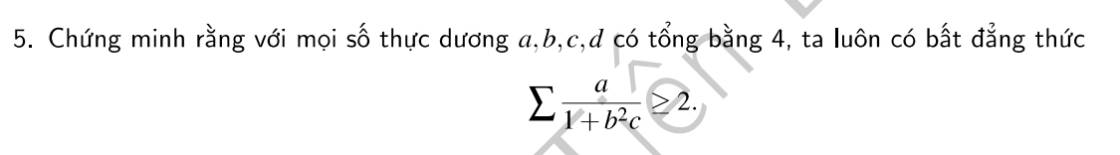\(a+b+c+d=4;a,b,c,d>0\)
Ta có:\(\sum\dfrac{a}{1+b^2c}=\sum\dfrac{a^2}{a+ab^2c}\ge\dfrac{\left(a+b+c+d\right)^2}{a+b+c+d+\sum ab^2c}=\dfrac{16}{4+\sum ab^2c}\)
Cần chứng minh \(\sum ab^2c\le4\). Để chứng minh BDT trên, ta chứng minh \(\left(xy+yz+zt+tx\right)\le\dfrac{\left(x+y+z+t\right)^2}{4}\left(1\right)\).
Thật vậy, bằng phép biến đổi tương đương, ta có:
\(x^2+y^2+z^2+t^2+2\left(xy+yz+zt+tx+xz+yt\right)\ge4\left(xy+yz+zt+tx\right)\)
\(\Leftrightarrow x^2+y^2+z^2+t^2-2\left(xy+yz+zt+tx\right)+2\left(xz+yt\right)\ge0\)
\(\Leftrightarrow\left(x+z\right)^2-2\left(x+z\right)\left(y+t\right)+\left(y+t\right)^2\ge0\)
\(\Leftrightarrow\left(x+z-y-t\right)^2\ge0\) (luôn đúng)
Vậy bất đẳng thức (1) đúng. Áp dụng bất đẳng thức (1), ta có:
\(\sum ab^2c\le\dfrac{\left(ab+bc+cd+da\right)^2}{4}\le\dfrac{\left[\dfrac{\left(a+b+c+d\right)^2}{4}\right]^2}{4}=4\)
Từ đây ta có điều phải chứng minh. Dấu "=" xảy ra khi \(a=b=c=d=1\)