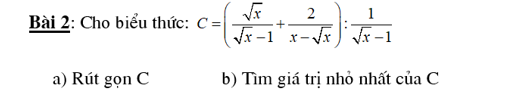\(1,ĐK:a\ge0;a\ne4\)
\(C=\dfrac{a}{a-16}-\dfrac{2}{\sqrt{a}-4}-\dfrac{2}{\sqrt{a}+4}\\ =\dfrac{a}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}-\dfrac{2\left(\sqrt{a}+4\right)}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}-\dfrac{2\left(\sqrt{a}-4\right)}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}\\ =\dfrac{a-2\sqrt{a}-8-2\sqrt{a}+8}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}\\ =\dfrac{a-4\sqrt{a}}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}\\ =\dfrac{\sqrt{a}\left(\sqrt{a}-4\right)}{\left(\sqrt{a}-4\right)\left(\sqrt{a}+4\right)}\\ =\dfrac{\sqrt{a}}{\sqrt{a}+4}\)
\(2,a=9-4\sqrt{5}=\left(\sqrt{5}-2\right)^2\\ \Rightarrow C=\dfrac{\sqrt{\left(\sqrt{5}-2\right)^2}}{\sqrt{\left(\sqrt{5}-2\right)^2}+4}\\ =\dfrac{\sqrt{5}-2}{\sqrt{5}-2+4}\\ =\dfrac{\sqrt{5}-2}{\sqrt{5}+2}=9-4\sqrt{5}\)










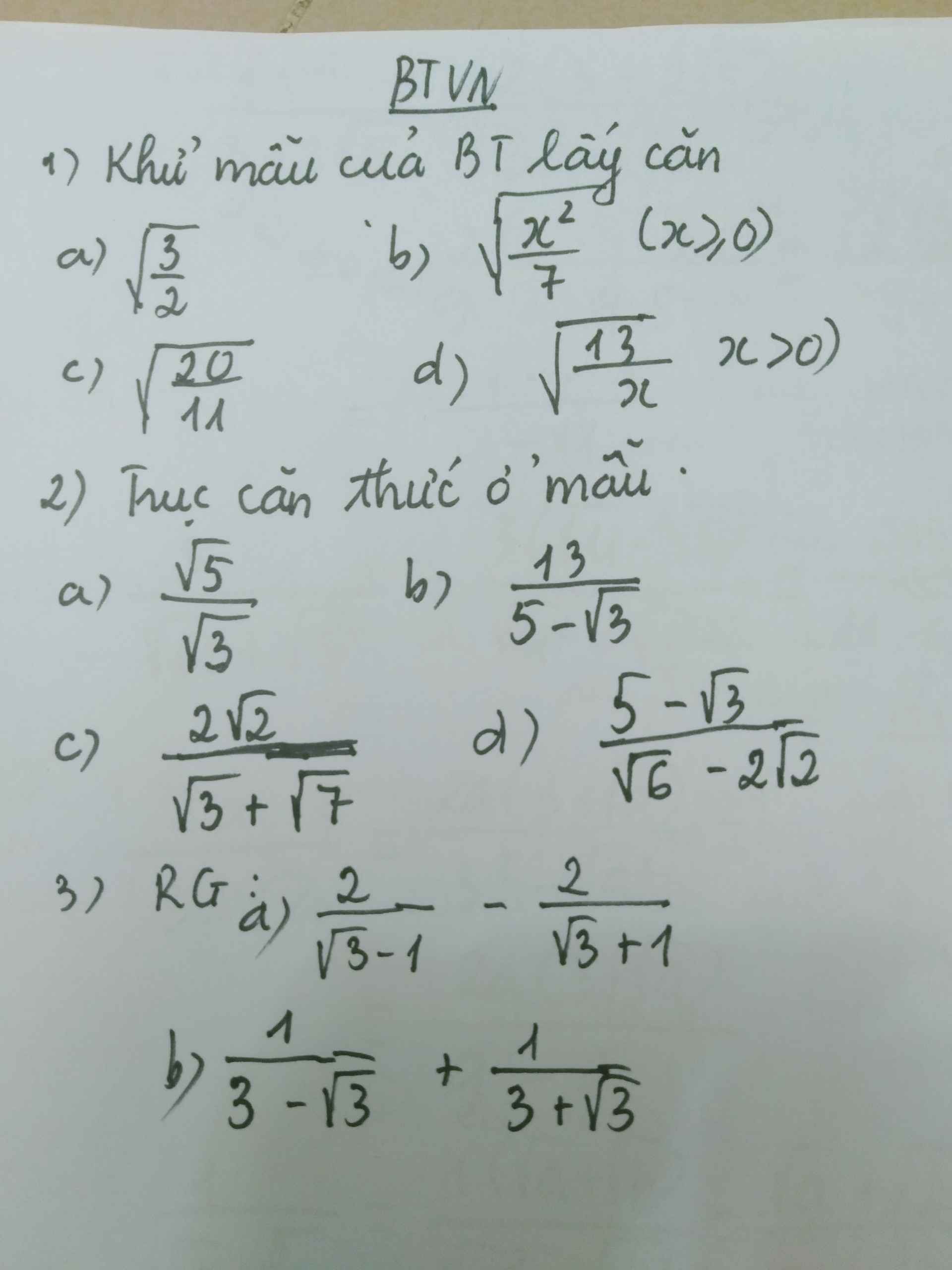

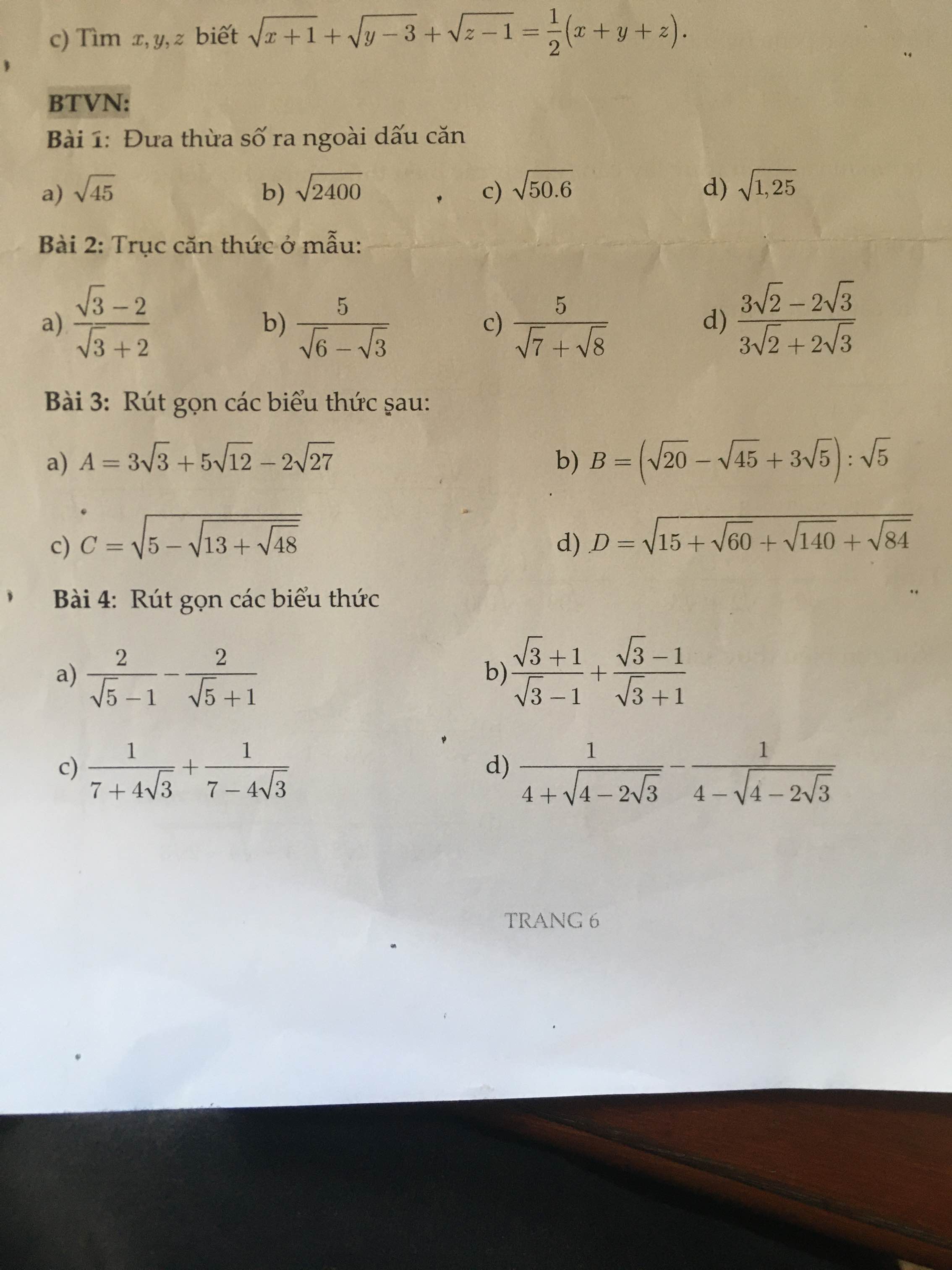

 HELP ME
HELP ME