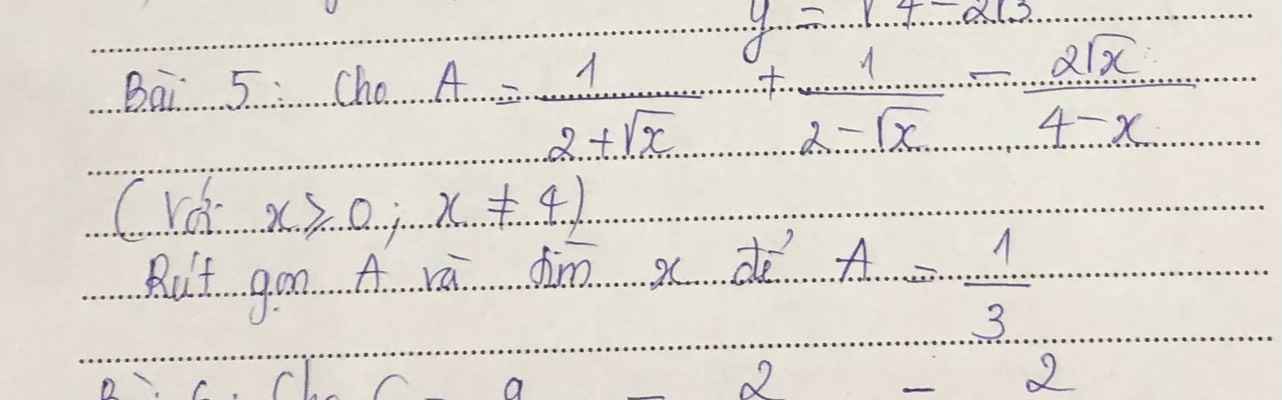\(A=\dfrac{1}{2+\sqrt{x}}+\dfrac{1}{2-\sqrt{x}}-\dfrac{2\sqrt{x}}{4-x}\\ =\dfrac{2-\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}+\dfrac{2+\sqrt{x}}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}-\dfrac{2\sqrt{x}}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\\ =\dfrac{2-\sqrt{x}+2+\sqrt{x}-2\sqrt{x}}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\\ =\dfrac{4-2\sqrt{x}}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\\ =\dfrac{2\left(2-\sqrt{x}\right)}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\\ =\dfrac{2}{2+\sqrt{x}}\\ A=\dfrac{1}{3}\Rightarrow\dfrac{2}{2+\sqrt{x}}=\dfrac{1}{3}\Rightarrow\sqrt{x}+2=6\\ \Rightarrow\sqrt{x}=4\Leftrightarrow x=16\left(tm\right)\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
help me,me cần gấp ạ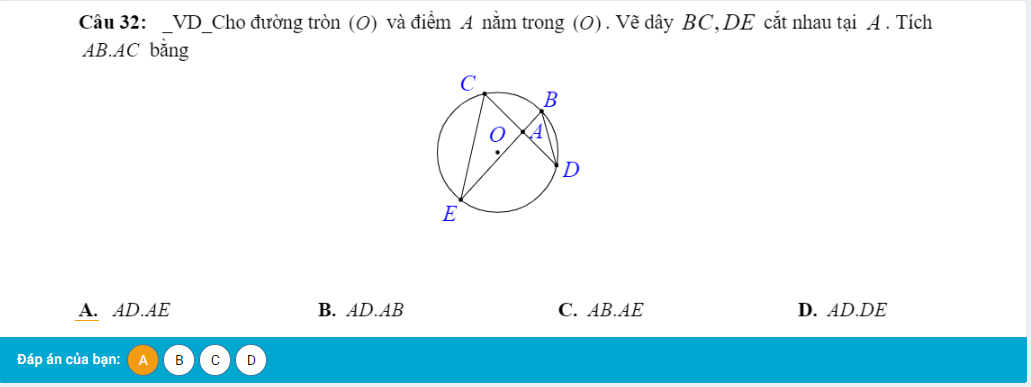
Help me với mn ơi
Giai pt giúp me
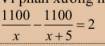
help me!!!!!
Đọc tiếp
help me!!!!!
Help me!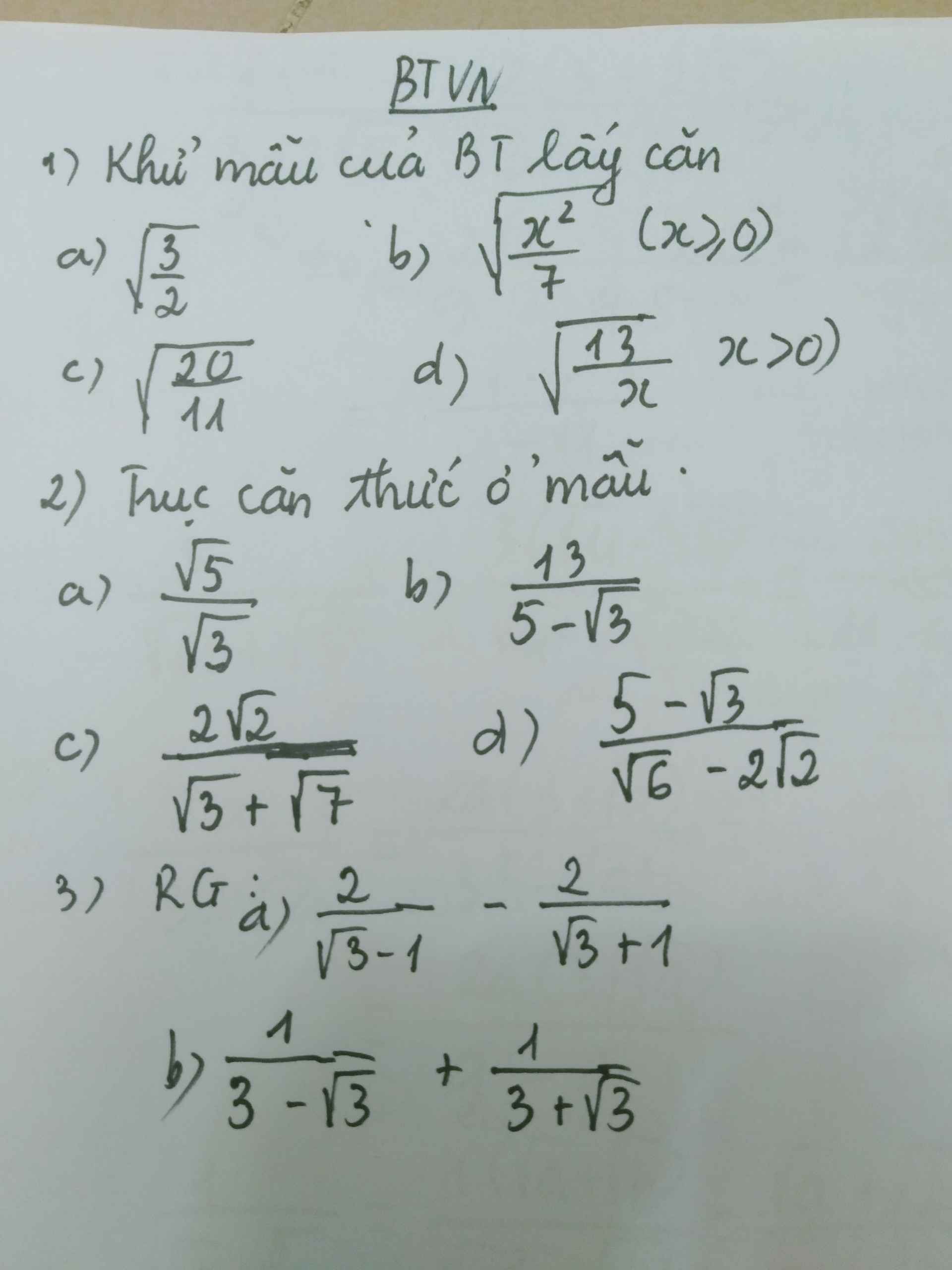
Help me!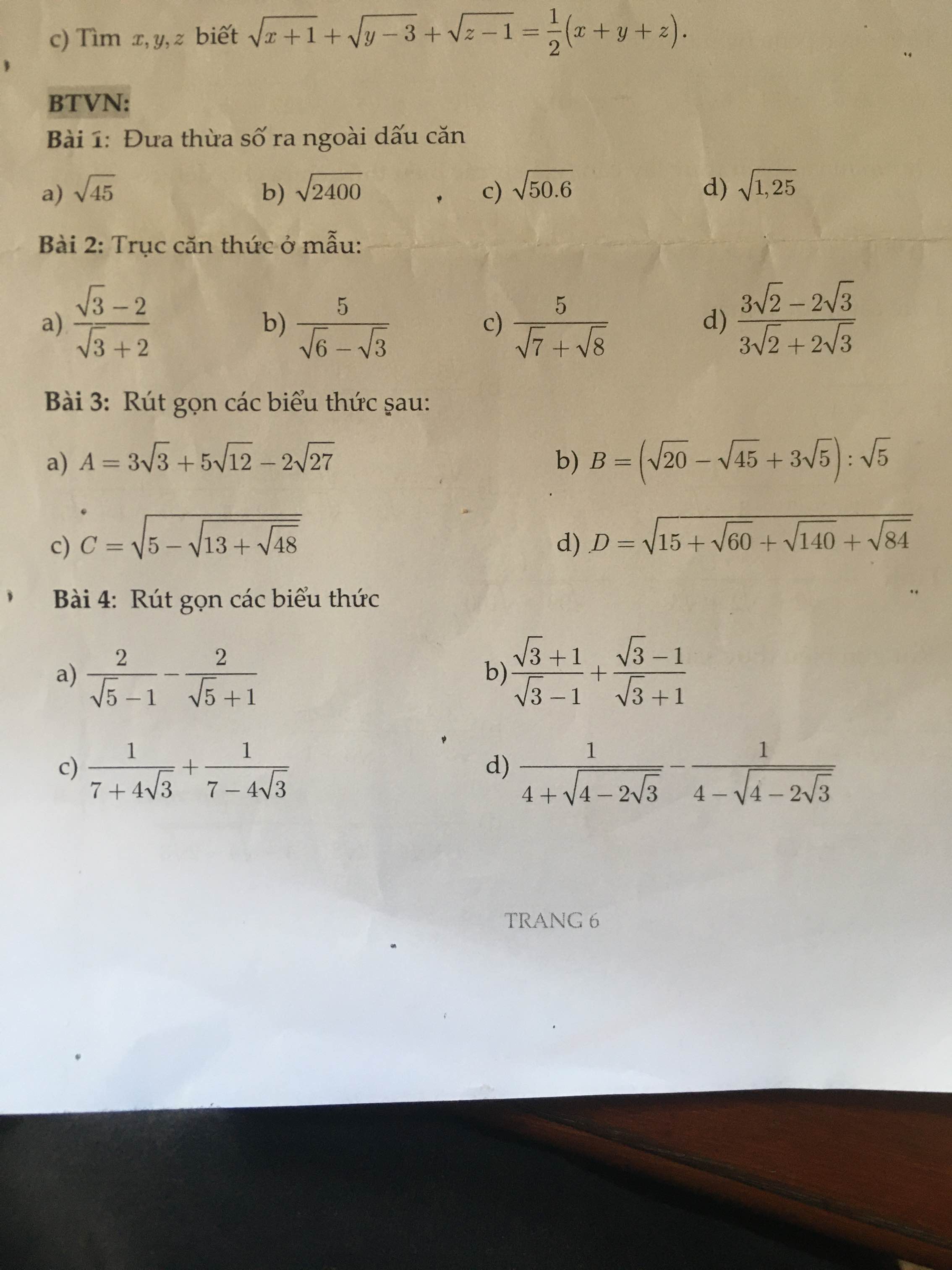
 HELP ME
HELP ME

HELP ME
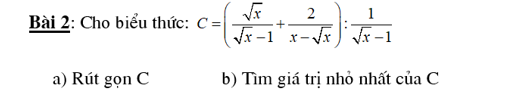
Help me
Help me
Help me