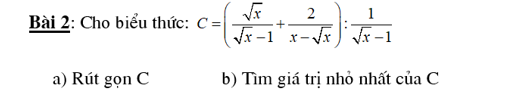\(1,P=\dfrac{\sqrt{x} }{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{3x+9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\\ =\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\\ =\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\\ =\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\\ =\dfrac{3}{\sqrt{x}+3}\)
\(2,P=\dfrac{1}{3}\Rightarrow\dfrac{3}{\sqrt{x}+3}=\dfrac{1}{3}\Rightarrow\sqrt{x}=6\Rightarrow x=36\left(tm\right)\)
3, Ta có:
\(\sqrt{x}\ge0\Rightarrow\sqrt{x}+3\ge3\Rightarrow P=\dfrac{3}{\sqrt{x}+3}\le1\)
Dấu "=" xảy ra: `x=0` (tm)
Vậy: ...







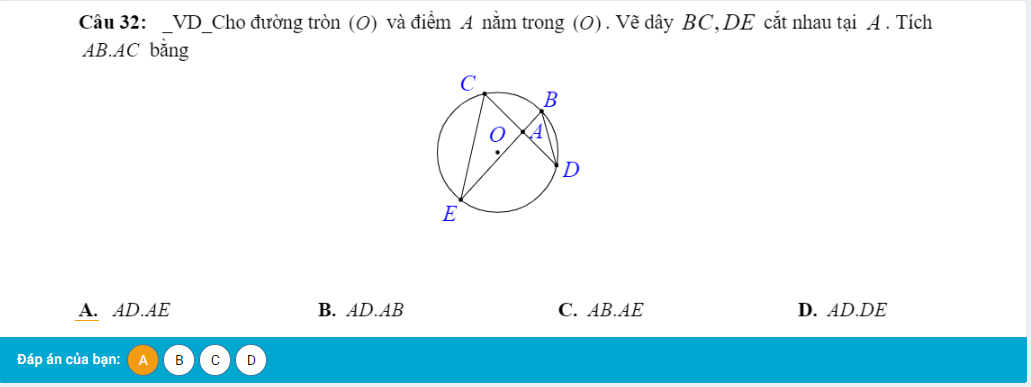

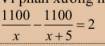


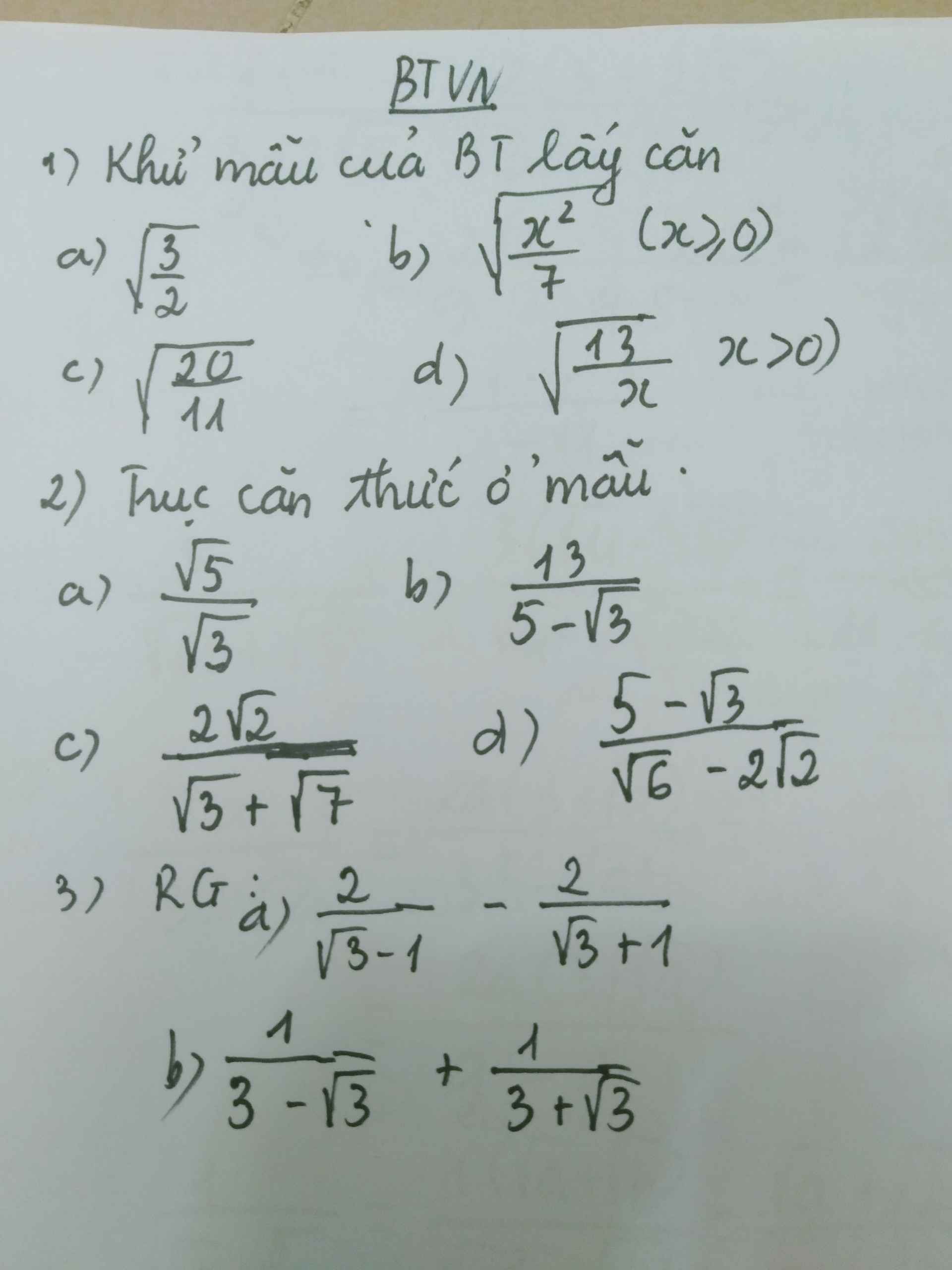


 HELP ME
HELP ME