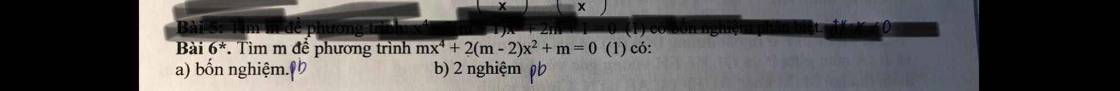Lời giải:
Đặt $x^2=t$ thì PT (1) trở thành:
$mt^2+2(m-2)t+m=0(*)$
Nếu $m=0$ thì PT(*) tương đương: $-4t=0\Leftrightarrow t=0\Leftrightarrow x=0$ (loại)
$\Rightarrow m\neq 0$
$\Rightarrow$ PT (*) là PT bậc 2.
a.
Để PT(1) có 4 nghiệm phân biệt thì PT $(*)$ phải có 2 nghiệm dương.
Điều này xảy ra khi mà:
\(\left\{\begin{matrix}
m\neq 0\\
\Delta'(*)=(m-2)^2-m^2>0\\
S=\frac{2(2-m)}{m}>0\\
P=\frac{m}{m}>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
m\neq 0\\
2m-2<0\\
\frac{2(2-m)}{m}>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
m\neq 0\\
m< 1\\
0< m< 2\end{matrix}\right.\Leftrightarrow 0< m< 1\)
b.
Để PT(1) có 4 nghiệm phân biệt thì PT $(*)$ có duy nhất 1 nghiệm dương. Điều này xảy ra khi mà:
TH1: PT(*) có 1 nghiệm kép dương.
\(\Leftrightarrow \left\{\begin{matrix}\\ m\neq 0\\ \Delta'(*)=(m-2)^2-m^2=0\\ S=\frac{2(2-m)}{m}>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}\\ m\neq 0\\ m=1\\ 0< m< 2\end{matrix}\right.\Leftrightarrow m=1\)
TH2: PT (*) có 1 nghiệm âm 1 nghiệm dương
\(\Leftrightarrow \left\{\begin{matrix}\\ m\neq 0\\ \Delta'(*)=(m-2)^2-m^2>0\\ P=\frac{m}{m}=1<0\end{matrix}\right. (\text{vô lý - loại})\)
Vậy $m=1$