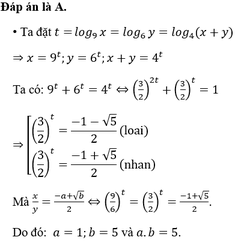Các câu hỏi tương tự
Gọi x, y là các số thực dương thỏa mãn
log
9
x
log
12
y
log
16
x
+
y
và
x
y
−
a
+
b
2
,
với a, b là hai số...
Đọc tiếp
Gọi x, y là các số thực dương thỏa mãn log 9 x = log 12 y = log 16 x + y và x y = − a + b 2 , với a, b là hai số nguyên dương. Tính P = a . b
A. P=6
B. P =5
C.P=8
D. P = 4
Cho các số thực dương x, y thỏa mãn:
x
+
y
5
4
thì biểu thức
S
4
x
+
1
4
y
đạt giá trị nhỏ nhất khi
x
a
y
b
thì a.b có giá trị là bao nhiêu?...
Đọc tiếp
Cho các số thực dương x, y thỏa mãn: x + y = 5 4 thì biểu thức S = 4 x + 1 4 y đạt giá trị nhỏ nhất khi x = a y = b thì a.b có giá trị là bao nhiêu?
A. a b = 3 8
B. a b = 25 64
C. a b = 0
D. a b = 1 4
Gọi x và y là các số thực dương thỏa mãn điều kiện
l
o
g
9
x
l
o
g
6
y
l
o
g
4
(
x
+
y
)
và
x
y
-
a
+
b
2...
Đọc tiếp
Gọi x và y là các số thực dương thỏa mãn điều kiện l o g 9 x = l o g 6 y = l o g 4 ( x + y ) và x y = - a + b 2 với a, b là hai số nguyên dương. Tính T = a + b
A. T = 6
B. T = 4
C. T = 11
D. T = 8
Gọi x, y là các số thực dương thỏa mãn điều kiện
log
9
x
log
6
x
log
4
x
+
y
và biết rằng
x
y
-
a
+
b
2
với a, b là...
Đọc tiếp
Gọi x, y là các số thực dương thỏa mãn điều kiện log 9 x = log 6 x = log 4 x + y và biết rằng x y = - a + b 2 với a, b là các số nguyên dương. Tính giá trị a + b
A. a + b = 6
B. a + b = 11
C. a + b = 4
D. a + b = 8
Gọi x, y là các số thực dương thỏa mãn
log
9
x
log
6
y
log
4
x
+
y
và
x
y
-
a
+
b
2
với a, b là hai số nguyên dươn...
Đọc tiếp
Gọi x, y là các số thực dương thỏa mãn log 9 x = log 6 y = log 4 x + y và x y = - a + b 2 với a, b là hai số nguyên dương. Tính tổng T = a + b
A. T = 6
B. T = 4
C. T = 11
D. T = 8
Gọi x, y là các số thực dương thỏa mãn
log
9
x
log
6
y
log
4
x
+
y
và
x
y
−
a
+
b
2...
Đọc tiếp
Gọi x, y là các số thực dương thỏa mãn log 9 x = log 6 y = log 4 x + y và x y = − a + b 2 , với a, b là hai số nguyên dương. Tính tổng T = a + b
A. T = 6
B. T = 4
C. T = 11
D. T = 8
Gọi số phức
z
a
+
b
i
a
,
b
∈
ℝ
thỏa mãn
z
−
1
1
v
à
1
+
i
z
¯...
Đọc tiếp
Gọi số phức z = a + b i a , b ∈ ℝ thỏa mãn z − 1 = 1 v à 1 + i z ¯ − 1 có phần thực bằng 1 đồng thời z không là số thực. Khi đó a . b bằng
A. a . b = 1
B. a . b = 2
C. a . b = − 2
D. a . b = − 1
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
-
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = - a + b 2 với a, b là các số nguyên dương. Tính a + b
A. 14
B. 3
C. 21
D. 32
Cho x, y là các số thực dương thỏa mãn
log
25
x
2
log
15
y
log
9
x
+
y
4
và
x
y
−
a
+
b...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn log 25 x 2 = log 15 y = log 9 x + y 4 và x y = − a + b 2 , với a, b là các số nguyên dương. Tính a+b
A. 14
B. 3
C. 21
D. 32