Đáp án A
Phương pháp: Logarit hai vế, đưa về phương trình bậc hai một ẩn.
Cách giải:
![]()
![]()
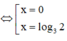
![]()
Đáp án A
Phương pháp: Logarit hai vế, đưa về phương trình bậc hai một ẩn.
Cách giải:
![]()
![]()
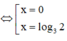
![]()
Gọi x 1 , x 2 là hai nghiệm của phương trình 9 x - 4 . 3 x + 3 = 0 Biết x 1 < x 2 tìm x 1
A. x 1 = 0
B. x 1 = 1
C. x 1 = - 1
D. x 1 = 2
Gọi x 1 ; x 2 là 2 nghiệm của phương trình 3 4 x + 8 − 4 .3 2 x + 5 + 27 = 0 . Tính S = x 1 . x 2
A. S = − 5 2
B. S = 3 2
C. S = 1
D. S = 3
Gọi x 1 , x 2 là hai nghiệm của phương trình x 2 - 3 x + 2 = 0 . Tính giá trị của A = 3 x 1 + 3 x 2
A. A=27.
B. A=28.
C. A=12.
D. A=9.
Gọi x 1 ; x 2 là hai nghiệm của phương trình 4 x 2 - x + 2 x 2 - x + 1 = 3 . Tính x 1 - x 2
A. 3
B. 0
C. 2
D. 1
Gọi x 1 , x 2 là hai nghiệm phân biệt của phương trình 4 x − 2 x + 3 + 15 = 0. Khi đó x 1 + x 2 bằng
A. log 2 15
B. 3
C. log 3 2 + log 5 2
D. log 2 3 5
Phương trình ( 2 x - 5 ) ( l o g 2 x - 3 ) = 0 có hai nghiệm x 1 , x 2 (với x 1 < x 2 ). Tính giá trị của biểu thức K = x 1 + 3 x 2
A. K = 32 + log 3 2
B. K = 18 + log 2 5
C. K = 24 + log 2 2
D. K = 32 + log 2 3
Gọi x 1 , x 2 là hai nghiệm của phương trình x 2 - 5 x + 6 = 0 Tính giá trị của A = 5 x 1 + 5 x 2
A. A = 125
B. A = 3125
C. A = 150
D. A = 15625
Gọi x 1 , x 2 x 1 < x 2 là nghiệm của phương trình 2.4 x − 5.2 x + 2 = 0. Khi đó hiệu x 2 − x 1 bằng
A.0
B. 2
C. -2
D. 3/2
Gọi x 1 , x 2 là hai nghiệm nguyên dương của bất phương trình log 2 1 + x < 2 . Tính giá trị của P = x 1 + x 2 .
A. 6
B. 4
C. 5
D. 3