
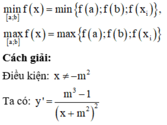
Hàm số bậc nhất trên bậc nhất luôn đồng biến hoặc nghịch biến trên từng khoảng xác định của nó.

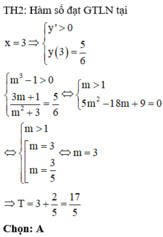

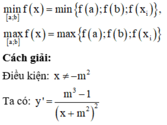
Hàm số bậc nhất trên bậc nhất luôn đồng biến hoặc nghịch biến trên từng khoảng xác định của nó.

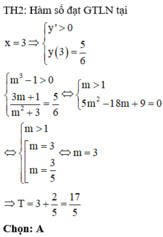
Gọi S là tập hợp các giá trị của tham số m để giá trị lớn nhất của hàm số y = x 2 − m x + 2 x − 2 trên đoạn [-1;1] bằng 3. Tính tổng tất cả các phần tử của S.
A. − 8 3
B. 5
C. 5 3
D. -1
Cho hàm số f(x)=(2 x +m)/(√x+1) với m là tham số thực, m>1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
A. 1
B. 3
C. 0
D. 2
Hình vẽ bên là đồ thị của hàm số y=f(x). Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số y = f x − 1 + m có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng
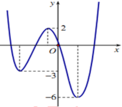
A. 12
B. 15
C. 18
D. 9
Gọi T là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số y = x 4 - 2 m x 2 + 1 đồng biến trên khoảng 2 ; + ∞ . Tổng giá trị các phần tử của T là
A. 8
B. 10
C. 4
D. 6
Hình vẽ bên là đồ thị của hàm số y = f(x). Gọi S là tập hợp các số nguyên dương của tham số m để hàm số y = |f(x – 1) + m| có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng:
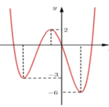
A. 12
B. 15
C. 18
D. 9
Cho hàm số y = - x 3 + m x 2 - ( m 2 + m + 1 ) x . Gọi S là tập hợp giá trị thực của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn [-1;1] bằng -6. Tính tổng các phần tử của S
A. 0.
B. 4.
C. -4
D. 2 2
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số y = x 3 − 3 x + m trên đoạn [0;2] bằng 3. Tập hợp S có bao nhiêu phần tử?
A. 1
B. 2
C. 6
D. 0
Biết rằng S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y = x 3 - 3(m-1) x 2 + 3m(m+2)x nghịch biến trên đoạn [0;1]. Tính tổng các phần tử của S?
A. S = 0.
B. S = 1.
C. S = -2.
D. S = -1.
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số y = x 3 − 3 x + m trên đoạn 0 ; 2 bằng 3. Số phần tử của S là:
A. 1
B. 2
C. 0
D. 6