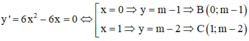
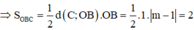
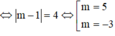
Đáp án B
Phương pháp:
Giải phương trình y’ = 0 tìm các điểm cực trị B, C của đồ thị hàm số và tính diện tích tam giác OBC.
Cách giải: TXĐ: D = R
Ta có:
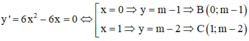
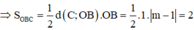
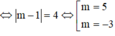
Cho hàm số y = - x 3 - 3 x 2 + 4 1 và đường tròn C : x - m 2 + y - m - 2 2 = 20 Biết rằng có hai giá trị m 1 , m 2 của tham số m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số (1) tiếp xúc với đường tròn (C). Tính tổng m 1 + m 2
A. -4
B. 10
C. 8
D. 0
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 - 3 m x 2 + 4 m 3 có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa độ
A. m = ± 1 2 4
B. m = ± 1
C. m = 1
D. m ≠ 0
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 − 3 m x 2 + 4 m 3 có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa độ.
A. m = ± 1 2 4 .
B. m = ± 1.
C. m = 1
D. m ≠ 0
Cho hàm số y = x 4 − 2 m 2 x 2 + m 2 có đồ thị (C) . Để đồ thị (C) có ba điểm cực trị A, B, C sao cho 4 điểm A, B, C, O là bốn đỉnh của hình thoi (O là gốc tọa độ) thì giá trị của tham số m là:
A. m = − 2
B. m = ± 2 2
C. m = ± 2
D. m = 2 2
Cho hàm số y = x 3 − 3 x 2 − m 2 − 2 x + m 2 có đồ thị là đường cong C . Biết rằng các số thực m 1 ; m 2 của tham số m để hai điểm cực trị của C và giao điểm của C với trục hoành tạo thành 4 đỉnh của hình chữ nhật. Tính T = m 1 4 + m 2 4
A. T = 22 − 12 2
B. T = 11 − 6 2
C. T = 3 2 − 2 2
D. T = 15 − 6 2 2
Gọi S là tập tất cả giá trị của tham số m để đồ thị hàm số y = x 4 - 2 m + 1 x 2 + m có ba điểm cực trị A, B, C sao cho OA=BC ; trong đó O là gốc tọa độ, A là điểm cực trị trên trục tung và B, C là hai điểm cực trị còn lại. Tích của tất cả các phần tử trong tập S bằng
A. 8
B. -8
C. 4
C. -4
Gọi S là tập hợp các giá trị thực của tham số m để hàm số y = x 3 − 3 m x 2 + 4 m 3 có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 (O là gốc tọa độ). Ta có tổng giá trị tất cả các phần tử của tập S bằng
A. 1
B. 2
C. -1
D. 0
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 − 3 m x 2 + 3 m 2 có hai điểm cực trị A, B mà Δ O A B có diện tích bằng 24 (O là gốc tọa độ)
A. m = 2
B. m = ± 1
C. m = ± 2
D. m = 1
Tìm tất cả giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 4 m 3 có hai điểm cực trị và B sao cho tam giác OAB có diện tích bằng 4, với O là gốc tọa độ
A. m = - 1 ; m = 1
B. m = 1
C. m ≢ 0
D. m = - 1 2 4 ; m = 1 2 4
