Chọn A.
Áp dụng công thức độ dài đuờng trung tuyến ta có
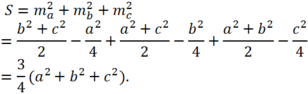
Chọn A.
Áp dụng công thức độ dài đuờng trung tuyến ta có
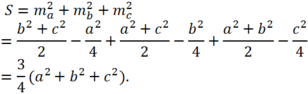
Cho tam giác ABC. Biết các cạnh a, b, c thoả mãn hệ thức: b(b2 - a2) = c(c2 - a2). Tìm mệnh đề đúng?
A. Tam giác ABC là tam giác đều
B. Tam giác ABC là tam giác cân
C. Tam giác ABC là tam giác tù
D. tam giác ABC là tam giác nhọn
Trong tam giác ABC. Chứng minh rằng
a) Góc A nhọn khi và chỉ khi a2 < b2 + c2
b) Góc A tù khi và chỉ khi a2 > b2 + c2
c) Góc A vuông khi và chỉ khi a2 = b2 + c2
Gọi S = \(m^2_a+m^2_b+m^2_c\) là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các mệnh đề sau mệnh đề nào đúng?
A. S = \(\dfrac{3}{4}\left(a^2+b^2+c^2\right)\)
B. S = \(a^2+b^2+c^2\)
D. S = 3\(\left(a^2+b^2+c^2\right)\)
C. S = \(\dfrac{3}{2}\left(a^2+b^2+c^2\right)\)
Cho a, b, c là độ dài ba cạnh của một tam giác.
a) Chứng minh (b - c)2 < a2
b) Từ đó suy ra: a2 + b2 + c2 < 2(ab + bc + ca)
Cho a, b, c là độ dài ba cạnh của tam giác. Sử dụng định lí về dấu tam thức bậc hai, chứng mình rằng:
b2x2 - (b2 + c2 - a2)x + c2 > 0 ∀x
Cho tam giác ABC biết các cạnh a, b, c thỏa mãn hệ thức: a(a2 – c2) = b(b2 – c2). Tính góc C.
A. 300
B. 600
C. 900
D. 1200
Cho tam giác ABC có a 2 = b 2 + c 2 - b c . Số đo của góc A là
A. 135 °
B. 150 °
C. 60 °
D. 120 °
Cho tam giác ABC có a 2 = b 2 + c 2 + 2 b c . Số đo của góc A là
A. 135 °
B. 45 °
C. 120 °
D. 150 °
Tính góc C của tam giác ABC biết c4 -2(a2+b2)c2+a4+a2b2 +b4=0
Cho tam giác ABC có a2 + b2 - c2 > 0. Khi đó :
A. Góc C > 900.
B. Góc C < 900.
C. Góc C = 900.
D. Không thể kết luận được gì về góc C.