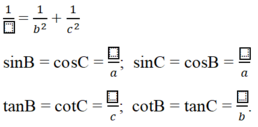Chọn C.
Theo đầu bài ta có; b(b2 - a2) = c(c2 - a2)
Hay b3 - c3 = a2(b - c)
Mà b - c ≠ 0 nên b2 + bc + c2 = a2
Theo định lí côsin thì a2 = b2 + c2 - 2bccosA
Do đó: b2 + bc + c2 = b2 + c2 - 2bccosA
Suy ra: cos A = - ½ hay góc A bằng 1200.
Cho tam giác ABC biết các cạnh a, b, c thỏa mãn hệ thức: a(a2 – c2) = b(b2 – c2). Tính góc C.
A. 300
B. 600
C. 900
D. 1200
Trong các mệnh đề sau
a. Nếu tam giác ABC thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC vuông tại B.
b. Nếu một phương trình bậc hai có biệt thức không âm thì nó có nghiệm.
c. Tam giác ABC là tam giác đều khi và chỉ khi nó thỏa mãn đồng thời hai điều kiện AB = AC và góc A = 600.
d. Hình thang cân có một trục đối xứng.
Các mệnh đề đúng là:
A. a, c.
B. a, b, c.
C. b, c.
D. b, c, d.
Cho tam giác ABC. Xét các mệnh đề dạng P ⇒ Q sau
a)Nếu ABC là một tam giác đều thì ABC là một tam giác cân.
b)Nếu ABC là một tam giác đều thì ABC là một tam giác cân và có một góc bằng 60o
Hãy phát biểu các mệnh đề Q ⇒ P tương ứng và xét tính đúng sai của chúng.
Cho tam giác ABC có điểm M thoả mãn |MA-MB-2MC|=|MA-MB|. Khẳng định nào sau đây là đúng?
A.tam giác ABC đều B,tam giác ABC cân tại C
C.tam giác ABC vuông tại C D.tam giác ABC cân tại B
Cho tam giác ABC thoả mãn hệ thức b + c = 2a. Trong các mệnh đề sau, mệnh đề nào đúng ?
A. cosB + cosC = 2cos A
B. sinB + sinC = 2sinA
C. sin C = cosA + sin B
D. sinB + cosA = cosC
Cho tam giác ABC thoả mãn b 2 + c 2 - a 2 = 3 b c . Khi đó :
A. A = 300
B. A = 900
C. A = 600
D. A = 1200
Trong tam giác ABC. Chứng minh rằng
a) Góc A nhọn khi và chỉ khi a2 < b2 + c2
b) Góc A tù khi và chỉ khi a2 > b2 + c2
c) Góc A vuông khi và chỉ khi a2 = b2 + c2
Cho tam giác ABC có \(\widehat{A}=2\widehat{B}\) , \(\widehat{C}\) tù và các cạnh đều là số nguyên dương. Tìm giá trị nhỏ nhất của chu vi tam giác ABC.
Tam giác ABC vuông tại A có đường cao AH = h và có BC = a, CA = b, AB = c. Gọi BH = c’ và CH = b’(h.2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:
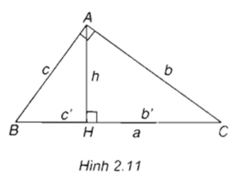
a2 = b2 + (.....)
b2 = a x (.....)
c2 = a x (.....)
h2 = b’ x (.....)
ah = b x (.....)
