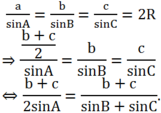Các câu hỏi tương tự
Cho A, B, C là 3 góc trong tam giác. Chứng minh rằng:1, sin A + sin B - sin C 4sindfrac{A}{2} sin dfrac{B}{2}sin dfrac{C}{2}2, dfrac{sinA+sinB-sinC}{cosA+cosB-cosC+1}tandfrac{A}{2}tandfrac{B}{2}tandfrac{C}{2} (ΔABC nhọn)3, dfrac{cosA+cosB+cosC+3}{sinA+sinB+sinC}tandfrac{A}{2}+tandfrac{B}{2}+tandfrac{C}{2}GIÚP MÌNH VỚI!!!
Đọc tiếp
Cho A, B, C là 3 góc trong tam giác. Chứng minh rằng:
1, sin A + sin B - sin C = 4sin\(\dfrac{A}{2}\) sin \(\dfrac{B}{2}\)sin \(\dfrac{C}{2}\)
2, \(\dfrac{sinA+sinB-sinC}{cosA+cosB-cosC+1}=tan\dfrac{A}{2}tan\dfrac{B}{2}tan\dfrac{C}{2}\) (ΔABC nhọn)
3, \(\dfrac{cosA+cosB+cosC+3}{sinA+sinB+sinC}=tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2}\)
GIÚP MÌNH VỚI!!!
Cho tam giác ABC thỏa mãn hệ thức b + c = 2a. Trong các mệnh đề sau, mệnh đề nào đúng?
A. CosB + Cos C = 2 Cos A B. Sin B + Sin C = 2 Sin A
C. Sin B + Sin C = \(\dfrac{1}{2}SinA\) D. Sin B + Sin C = 2 Sin A
Tìm tính chất của tam giác ABC thỏa:
sinA+sinB+sinC=1-cosA+cosB+cosC
Cho tam giác ABC có góc A tù. Cho các biểu thức sau: (1) M sin A + sin B + sin C (2) N cosA. cosB. cosC (3)
P
cos
A
2
.
sin
B
2
.
c
o
t
C
2
(4) Q cotA.tan B.tan C Số các b...
Đọc tiếp
Cho tam giác ABC có góc A tù. Cho các biểu thức sau:
(1) M = sin A + sin B + sin C
(2) N = cosA. cosB. cosC
(3) P = cos A 2 . sin B 2 . c o t C 2
(4) Q = cotA.tan B.tan C
Số các biểu thức mang giá trị dương là:
A. 1
B. 2
C. 3
D. 4
Cho tam giác ABC thỏa mãn: sinC = cosA + cosB. Tìm mệnh đề đúng
A. Tam giác ABC cân tại A
B. Tam giác ABC là tam giác nhọn
C. Tam giác ABC đều
D. Tam giác ABC là tam giác vuông.
Cho tam giác ABC thỏa mãn sin2A = sinB. sinC. Hỏi mệnh đề nào đúng.
A. a2 = bc
B. cosA ≥ ½
C. Cả A và B sai
D. Cả A và B đúng
Hãy chứng minh công thức sin(a + b) = sina cosb + cosa sinb.
Cho tam giác ABC. Biết các cạnh a, b, c thoả mãn hệ thức: b(b2 - a2) c(c2 - a2). Tìm mệnh đề đúng? A. Tam giác ABC là tam giác đều B. Tam giác ABC là tam giác cân C. Tam giác ABC là tam giác tù D. tam giác ABC là tam giác nhọn
Đọc tiếp
Cho tam giác ABC. Biết các cạnh a, b, c thoả mãn hệ thức: b(b2 - a2) = c(c2 - a2). Tìm mệnh đề đúng?
A. Tam giác ABC là tam giác đều
B. Tam giác ABC là tam giác cân
C. Tam giác ABC là tam giác tù
D. tam giác ABC là tam giác nhọn
Hãy nhắc lại định lí côsin trong tam giác. Từ các hệ thức này hãy tính cosA, cosB, cosC theo các cạnh của tam giác.