
giúp vs ạa
Câu 2. Hàng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu \( h \) của mực nước trong kênh tính theo thời gian \( t \) trong một ngày \((0 \leq t \leq 24)\) cho bởi công thức \( h = 3 \cos \left( \frac{\pi}{6} t + \pi \right) + 10 \). Có bao nhiêu thời điểm mực nước cao nhất trong một ngày.
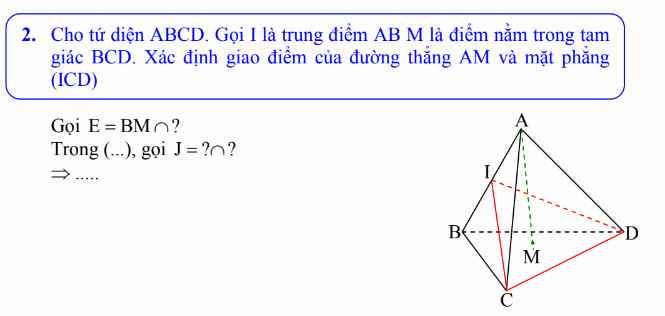
Câu 3. Cho tứ diện \( ABCD \) và \( G \) là trọng tâm tam giác \( BCD \). Lấy \( P \) trung điểm cạnh \( AD \), \( H \) là giao điểm của mặt phẳng \( (ABG) \) với cạnh \( CP \), \( E \) là giao điểm \( BH \) và \( AG \). Khi đó tỉ lệ \( \frac{AE}{AG} \) là bao nhiêu?
Câu 2: Ta có: \(-1\le cos\left(\frac{\pi}{6}\cdot t+\pi\right)\le1\)
=>\(-3\le3\cdot cos\left(\frac{\pi}{6}\cdot t+\pi\right)\le3\)
=>\(-3+10\le3\cdot cos\left(\frac{\pi}{6}\cdot t+\pi\right)+10\le3+10\)
=>7<=h<=13
=>Để mực nước lên cao nhất thì h=13
=>\(cos\left(\frac{\pi}{6}\cdot t+\pi\right)=1\)
=>\(\frac{\pi}{6}\cdot t+\pi=k2\pi\)
=>\(\frac{t}{6}+1=2k\)
=>\(\frac{t}{6}=2k-1\)
=>t=12k-6
0<=t<=24
=>0<=12k-6<=24
=>6<=12k<=30
=>1/2<=k<=5/2
mà k nguyên
nên k∈{1;2}
=>Có 2 thời điểm để mực nước lên cao nhất










 giúp vs
giúp vs giúp vs
giúp vs



