\(\dfrac{1+sin2x}{cos2x}=\dfrac{\left(sinx+cosx\right)^2}{\left(cos^2x-sin^2x\right)}=\dfrac{\left(cosx+sinx\right)^2}{\left(cosx-sinx\right)\left(cosx+sinx\right)}\)
\(=\dfrac{cosx+sinx}{cosx-sinx}\)(1)
\(\dfrac{1+tanx}{1-tanx}=\dfrac{1+\dfrac{sinx}{cosx}}{1-\dfrac{sinx}{cosx}}=\dfrac{sinx+cosx}{cosx}:\dfrac{cosx-sinx}{cosx}\)
\(=\dfrac{sinx+cosx}{cosx}\cdot\dfrac{cosx}{cosx-sinx}=\dfrac{sinx+cosx}{cosx-sinx}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{1+tanx}{1-tanx}=\dfrac{1+sin2x}{cos2x}\)
Đúng 2
Bình luận (0)







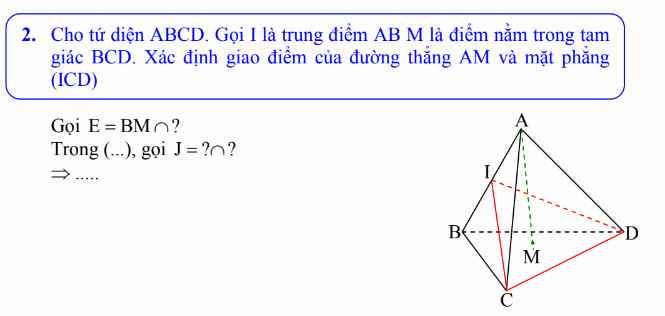 giúp vs
giúp vs giúp vs
giúp vs




