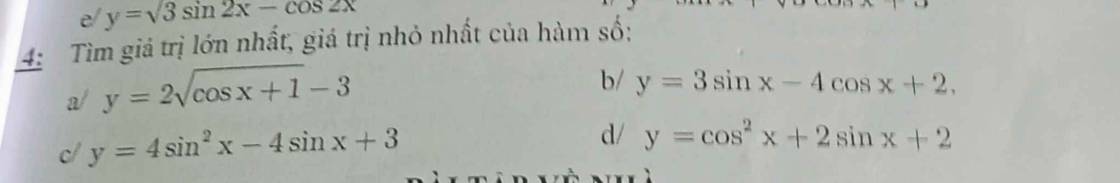a) Có \(1\ge cosx\ge-1\)
\(\Leftrightarrow2\ge cosx+1\ge0\)
\(\Leftrightarrow\sqrt{2}\ge\sqrt{cosx+1}\ge0\)
\(\Leftrightarrow2\sqrt{2}-3\ge y\ge-3\)
\(miny=-3\Leftrightarrow cosx=-1\Leftrightarrow x=\pi+k2\pi\)
\(maxy=2\sqrt{2}-3\Leftrightarrow cosx=1\Leftrightarrow x=k2\pi\)
Vậy...
b) \(y=5\left(\dfrac{3}{5}sinx-\dfrac{4}{5}cosx\right)+2\)
Đặt \(cosu=\dfrac{3}{5}\Rightarrow sinu=\dfrac{4}{5}\)
\(y=5\left(sinx.cosu-cosx.sinu\right)+2\)
\(=5sin\left(x-u\right)+2\in\left[-3;7\right]\)
\(miny=-3\Leftrightarrow sin\left(x-u\right)=-1\Leftrightarrow x-u=-\dfrac{\pi}{2}+k2\pi\)\(\Leftrightarrow x=arccos\left(\dfrac{3}{5}\right)-\dfrac{\pi}{2}+k2\pi\)
\(maxy=7\Leftrightarrow sin\left(x-u\right)=1\Leftrightarrow x-u=\dfrac{\pi}{2}+k2\pi\)\(\Leftrightarrow x=acrcos\left(\dfrac{3}{5}\right)+\dfrac{\pi}{2}+k2\pi\)
c) Đặt \(t=sinx,t\in\left[-1;1\right]\)
\(y=4t^2-4t+3\)
\(y'=0\Leftrightarrow8t-4=0\Leftrightarrow t=\dfrac{1}{2}\)
Vẽ BBT, từ đó suy ra \(miny=2\Leftrightarrow t=\dfrac{1}{2}\Leftrightarrow sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\) ( k nguyên)
\(maxy=11\Leftrightarrow t=-1\Leftrightarrow sinx=-1\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\) ( k nguyên)
Vậy...
d)\(y=cos^2x+2sinx+2\)
\(=1-sin^2x+2sinx+2\)
\(=-sin^2x+2sinx+3\)
Đặt \(t=sinx,t\in\left[-1;1\right]\)
\(y=-t^2+2t+3\Rightarrow y'=0\Leftrightarrow t=1\)
Vẽ BBT, suy ra \(miny=0\Leftrightarrow t=-1\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(maxy=4\Leftrightarrow t=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
Vậy...