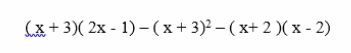-ĐKXĐ: \(x\ne\pm\dfrac{1}{2}\).
\(\dfrac{5}{2x+1}-\dfrac{2x}{1-2x}=1-\dfrac{2\left(3-2x\right)}{4x^2-1}\)
\(\Leftrightarrow\dfrac{5}{2x+1}+\dfrac{2x}{2x-1}=1-\dfrac{2\left(3-2x\right)}{\left(2x+1\right)\left(2x-1\right)}\)
\(\Leftrightarrow\dfrac{5\left(2x-1\right)}{\left(2x+1\right)\left(2x-1\right)}+\dfrac{2x\left(2x+1\right)}{\left(2x+1\right)\left(2x-1\right)}=\dfrac{\left(2x+1\right)\left(2x-1\right)}{\left(2x+1\right)\left(2x-1\right)}-\dfrac{2\left(3-2x\right)}{\left(2x+1\right)\left(2x-1\right)}\)
\(\Rightarrow10x-5+4x^2+2x=4x^2-1-6+4x\)
\(\Leftrightarrow4x^2-4x^2+10x+2x-4x=-1-6+5\)
\(\Leftrightarrow8x=-2\)
\(\Leftrightarrow x=\dfrac{-1}{4}\left(nhận\right)\)
-Vậy \(S=\left\{-\dfrac{1}{4}\right\}\)
\(\Leftrightarrow\dfrac{5}{2x+1}-\left(-\dfrac{2x}{2x+1}\right)=1-\dfrac{2\left(3-2x\right)}{\left(2x-1\right)\left(2x+1\right)}\)
\(\Leftrightarrow5\left(2x-1\right)-\left[-2x\left(2x-1\right)\right]=\left(2x-1\right)\left(2x+1\right)-2\left(3-2x\right)\)
\(\Leftrightarrow10x-5-\left(-4x^2+2x\right)=4x^2-1-6+4x\)
\(\Leftrightarrow10x-5+4x^2-2x=4x^2-7+4x\)
\(\Leftrightarrow4x=-2\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
giúp em với mn ơi,e đag cần gấp, mn giúp em với ạ
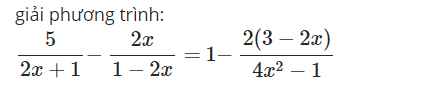
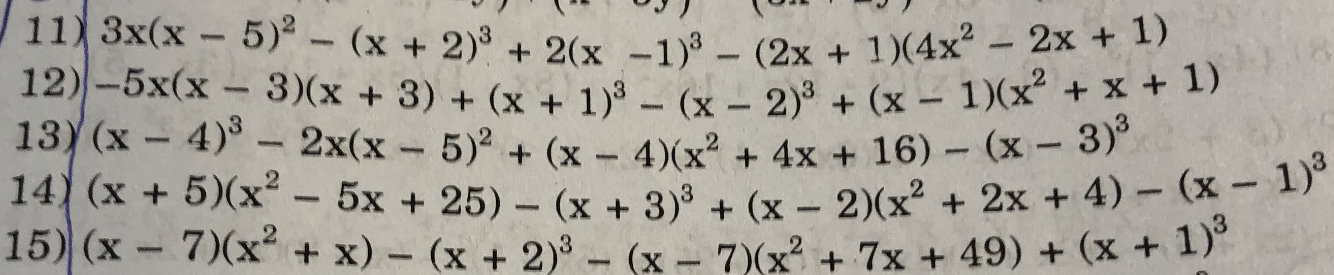
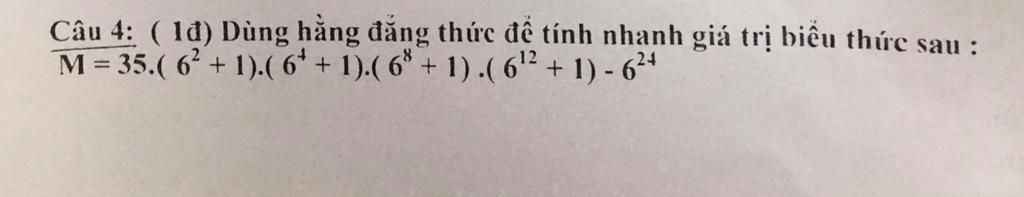
giúp mik với mn ơi 
