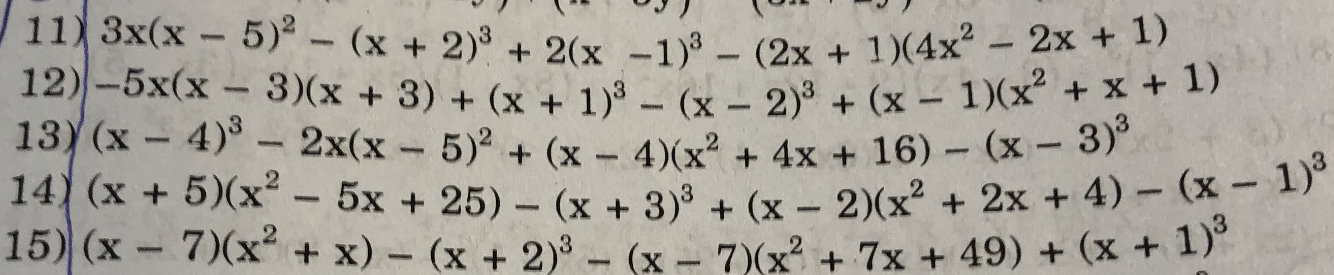Question

giúp em với mn ơi

Answer 1

a. Áp dụng BĐT Bunhiacopxky:

$\text{VT}^2\leq [(a+2)+(b+2)+(c+2)](1+1+1)=3(a+b+c+6)=3.12=36$

$\Rightarrow \text{VT}\leq 6$ (đpcm)

Dấu "=" xảy ra khi $a=b=c=2$

b.

Áp dụng BĐT Cô-si:

$\text{VT}\leq \frac{a+3b+8+8}{12}+\frac{b+3c+8+8}{12}+\frac{c+3a+8+8}{12}=\frac{a+b+c}{3}+4=\frac{6}{3}+4=6$

Ta có đpcm

Dấu "=" xảy ra khi $a=b=c=2$

Answer 2

c. Áp dụng BĐT Cô-si:

\(\text{VT}\leq \frac{9a+a(b+7)}{6}+\frac{9b+b(c+7)}{6}+\frac{9c+c(a+7)}{6}=\frac{16(a+b+c)}{6}+\frac{ab+bc+ac}{6}=16+\frac{ab+bc+ac}{6}\)

Cũng áp dụng BĐT Cô-si:

$ab+bc+ac\leq \frac{(a+b+c)^2}{3}=\frac{6^2}{3}=12$

$\Rightarrow \text{VT}\leq 16+\frac{12}{6}=18$ (đpcm)

Dấu "=" xảy ra khi $a=b=c=2$
d.

Áp dụng BĐT Cô-si:
\(\text{VT}\leq \frac{4a+(b+6)}{4}+\frac{4b+(c+6)}{4}+\frac{4c+(a+6)}{4}=\frac{5(a+b+c)+18}{4}=\frac{30+18}{4}=12\) (đpcm)

Dấu "=" xảy ra khi $a=b=c=2$

e.

Áp dụng BĐT Cô-si:
\(\text{VT}\leq \frac{a+6+8+8}{12}+\frac{b+6+8+8}{12}+\frac{c+6+8+8}{12}=\frac{a+b+c+66}{12}=\frac{6+66}{12}=\frac{72}{12}=6\) (đpcm)

Dấu "=" xảy ra khi $a=b=c=2$

Answer 3

Câu a bạn có thể sử dụng BĐT Bunhiacopxky như ở dưới, không thì xài BĐT Cô-si cũng được:

\(\text{VT}\leq \frac{(a+2)+4}{4}+\frac{(b+2)+4}{4}=\frac{(c+2)+4}{4}=\frac{a+b+c+18}{4}=\frac{6+18}{4}=6\) (đpcm)

Dấu "=" xảy ra khi $a=b=c=2$