1: Ta có: ΔOAC cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)AC và OI là phân giác của góc AOC
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)CB tại C
Ta có: OI\(\perp\)AC
CB\(\perp\)AC
Do đó: OI//CB
2: Xét ΔOAD và ΔOCD có
OA=OC
\(\widehat{DOA}=\widehat{DOC}\)
OD chung
Do đó: ΔOAD=ΔOCD
=>\(\widehat{OAD}=\widehat{OCD}\)
=>\(\widehat{OAD}=90^0\)
=>DA là tiếp tuyến của (O)
3: Ta có: OC\(\perp\)DK
KB\(\perp\)KD
Do đó: OC//KB
=>\(\widehat{KBC}=\widehat{OCB}\)(hai góc so le trong)
mà \(\widehat{OCB}=\widehat{OBC}\)(ΔOBC cân tại O)
nên \(\widehat{KBC}=\widehat{OBC}\)
Xét ΔBHC vuông tại H và ΔBKC vuông tại K có
BC chung
\(\widehat{HBC}=\widehat{KBC}\)
Do đó: ΔBHC=ΔBKC
=>CH=CK
Xét ΔCAB vuông tại C có CH là đường cao
nên \(CH^2=HA\cdot HB\)
=>\(CK^2=HA\cdot HB\)
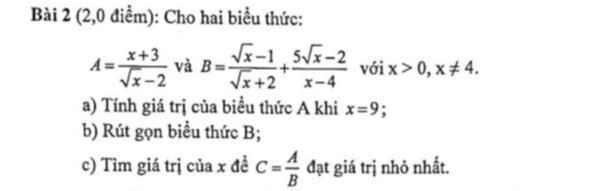mn giúp mik câu c vs ạ
