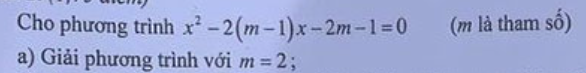`a,` Thay `m=2` vào phương trình ta có:
`x^2 -2(2-1)x-2.2-1=0`
`<=>x^2 -2.1x-4-1=0`
`<=>x^2 -2x-5=0`
Ta có:
`Δ=b^2 -4ac`
`=(-2)^2 -4.1.(-5)`
`=4+20`
`=24>0`
Suy ra phương trình luôn có 2 nghiệm phân biệt
\(\Rightarrow x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(-2\right)+\sqrt{24}}{2.1}=\dfrac{2+2\sqrt{6}}{2}=1+\sqrt{6}\\ x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-2\right)-\sqrt{24}}{2.1}=\dfrac{2-2\sqrt{6}}{2}=1-\sqrt{6}\)
Vậy ...
Với \(m=2\) thay vào pt, ta được:
\(x^2-2\left(2-1\right)x-2.2-1=0\)
\(\Leftrightarrow x^2-2x-5=0\)
Ta có: \(\Delta'=\left(-1\right)^2=-\left(-5\right)=6>0\)
\(\Rightarrow\) Pt có 2 nghiệm phân biệt \(\left[{}\begin{matrix}x=1+\sqrt{6}\\x=1-\sqrt{6}\end{matrix}\right.\)
Vậy với \(m=2\), pt có tập nghiệm là \(S=\left\{1-\sqrt{6};1+\sqrt{6}\right\}\)
Thay m = 2 vào pt, ta được:
\(x^2-2\left(2-1\right)x-2.2-1=0
\)
⇔ \(x^2-2x-5\)
\(\Delta=b^2-4ac\)
⇔ \(\Delta=\left(-2\right)^2-4.1.\left(-5\right)\)
⇔ \(\Delta=24>0\Rightarrow\sqrt{\Delta}=2\sqrt{6}\)
⇒ Vậy pt có 2 nghiệm phân biệt
\(\)\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{2+2\sqrt{6}}{2}=1+\sqrt{6}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{2-2\sqrt{6}}{2}=1-\sqrt{6}\)
vậy \(x_1=1+\sqrt{6};x_2=1-\sqrt{6}\)