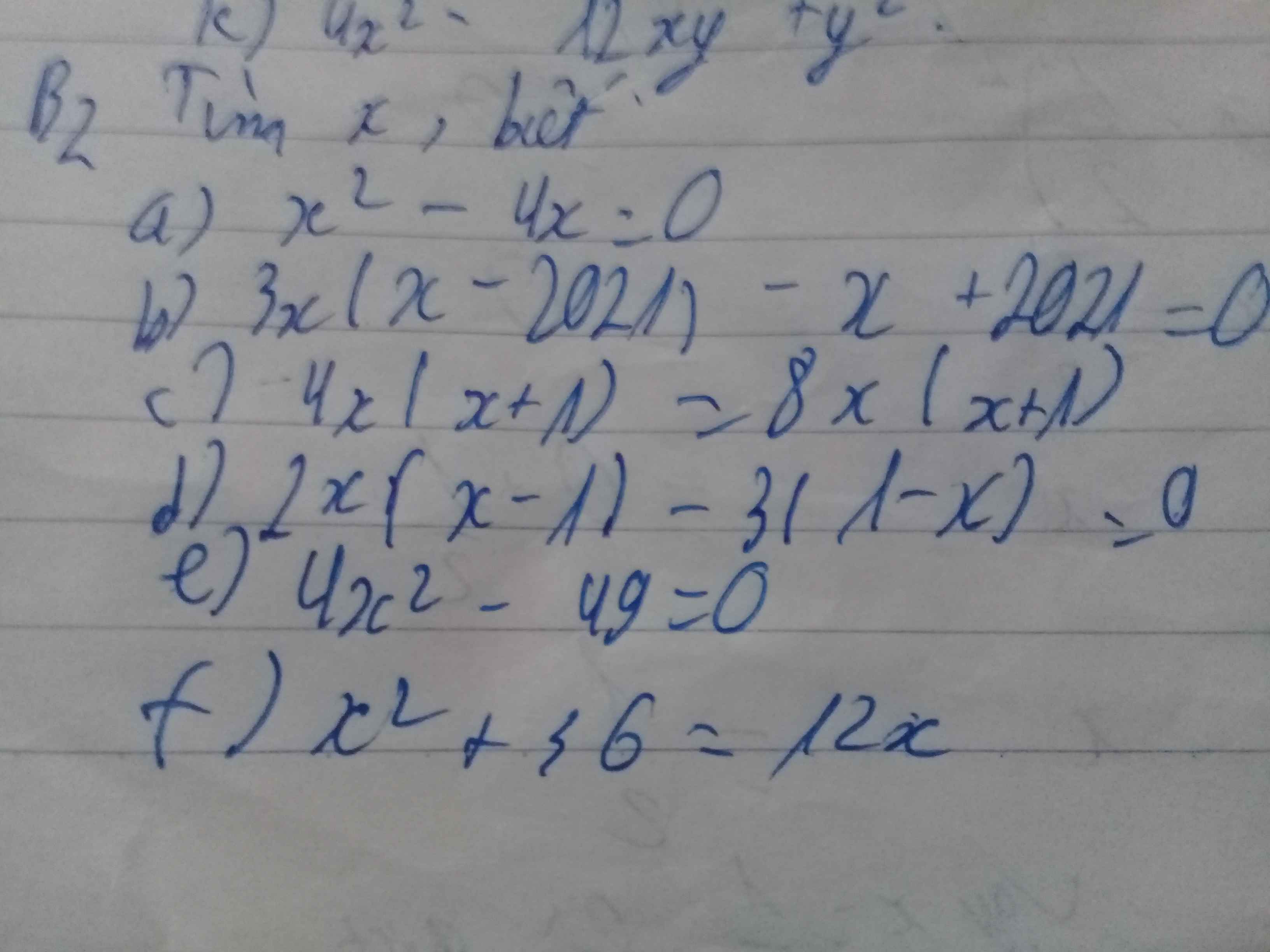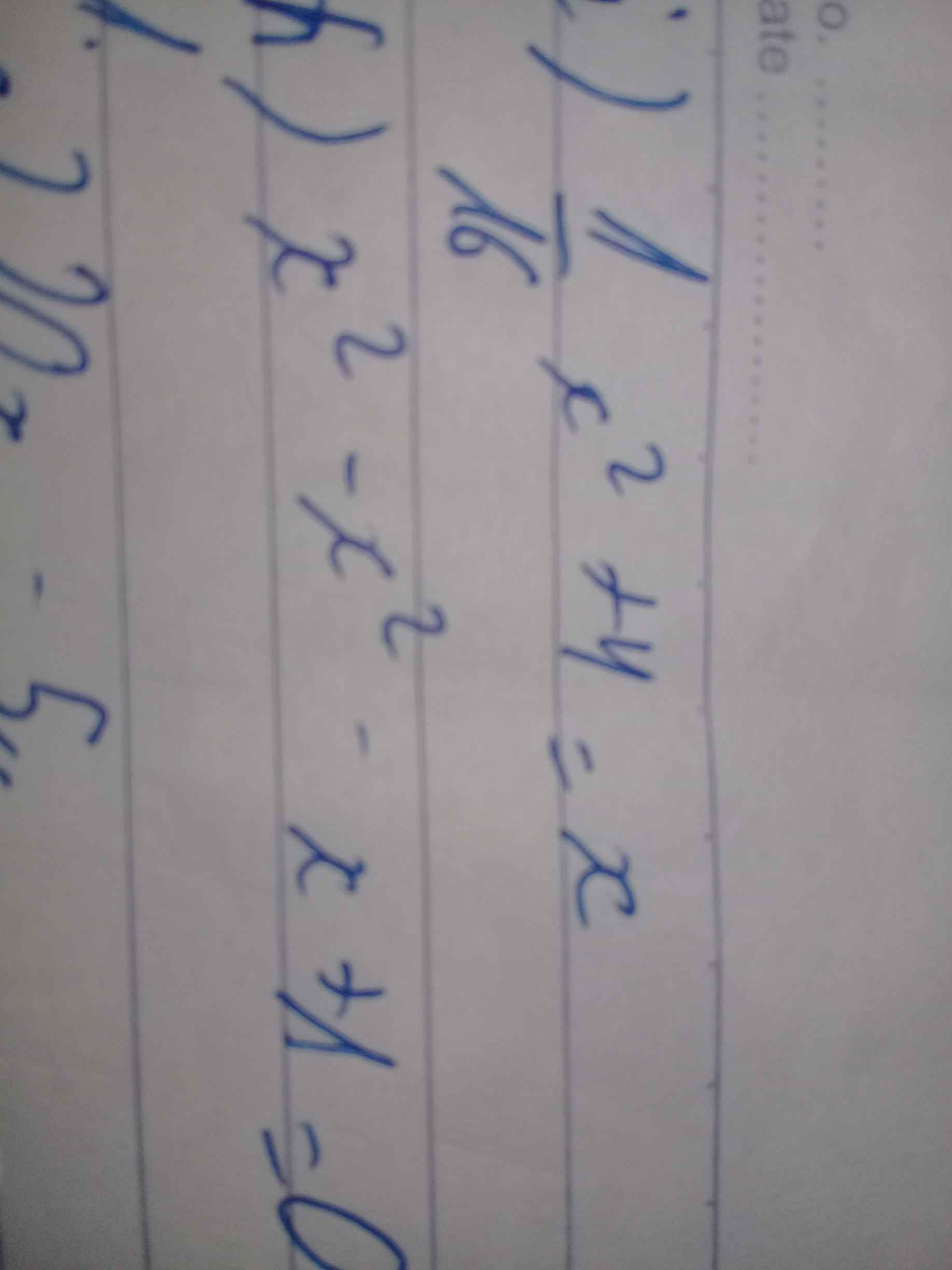Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔABC
Suy ra: ED//BC và \(ED=\dfrac{BC}{2}\)
Xét tứ giác BEDC có ED//BC
nên BEDC là hình thang
Hình thang BEDC có
M là trung điểm của EB
N là trung điểm của DC
Do đó: MN là đường trung bình của hình thang BEDC
Suy ra: MN//ED//BC và \(MN=\dfrac{1}{2}\left(ED+BC\right)=\dfrac{1}{2}\cdot\dfrac{3}{2}BC=\dfrac{3}{4}BC\)
Xét ΔEBD có
M là trung điểm của EB
MI//ED
Do đó: I là trung điểm của ED
Xét ΔEDC có
N là trung điểm của DC
NK//ED
Do đó: K là trung điểm của EC
Xét ΔBED có
M là trung điểm của EB
I là trung điểm của BD
Do đó: MI là đường trung bình của ΔBED
Suy ra: \(MI=\dfrac{ED}{2}=\dfrac{1}{4}BC\)(1)
Xét ΔCED có
N là trung điểm của DC
K là trung điểm của EC
Do đó: NK là đường trung bình của ΔCED
Suy ra: \(NK=\dfrac{ED}{2}=\dfrac{1}{4}BC\)(2)
Ta có: MI+IK+NK=MN
nên \(IK=\dfrac{1}{4}BC\left(3\right)\)
Từ (1), (2) và (3) suy ra MI=IK=KN
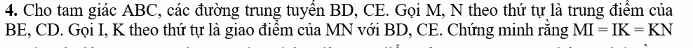
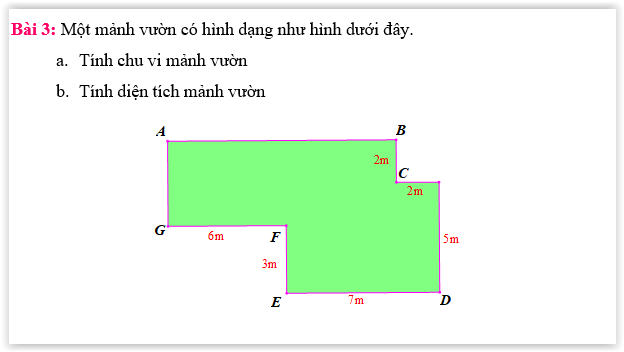
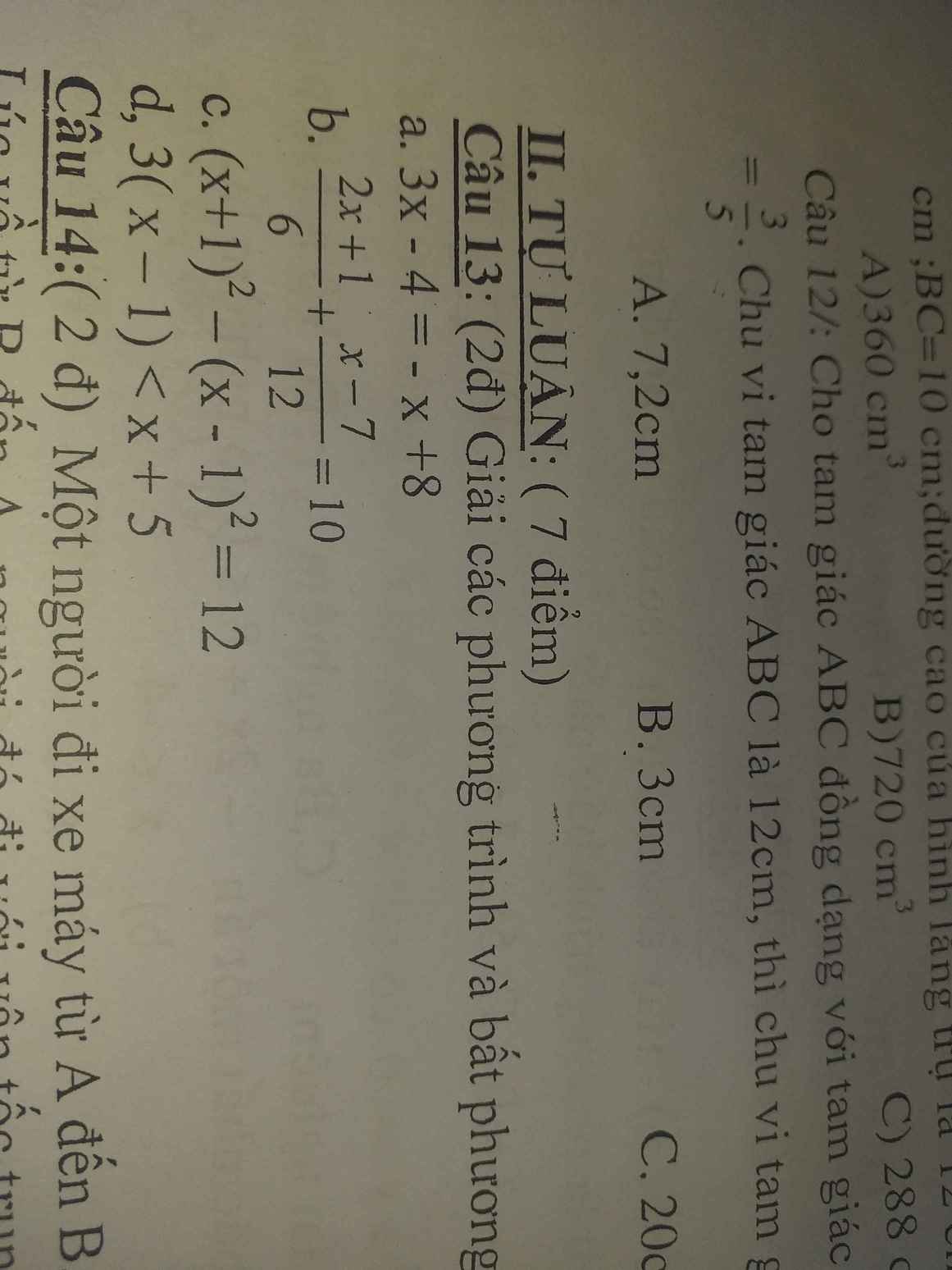
giúp mk vs ạ ai nhanh mk tick nha 
