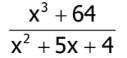\(\dfrac{x^3+64}{x^2+5x+4}\)
\(=\dfrac{\left(x+4\right)\left(x^2-4x+16\right)}{x^2+4x+x+4}=\dfrac{\left(x+4\right)\left(x^2-4x+16\right)}{x\left(x+4\right)+\left(x+4\right)}=\dfrac{\left(x+4\right)\left(x^2-4x+16\right)}{\left(x+4\right)\left(x+1\right)}=\dfrac{x^2-4x+16}{x+1}\)
(x³ + 64) : (x² + 5x + 4)
= [(x + 4)(x² - 4x + 16)] : (x² + x + 4x + 4)
=[(x + 4)(x² - 4x + 16)] : [(x² + x) + (4x + 4)]
= [(x + 4)(x² - 4x + 16)] : [x(x + 1) + 4(x + 1)]
= [(x + 4)(x² - 4x + 16)] : [(x + 1)(x + 4)]
= (x² - 4x + 4) : (x + 1)