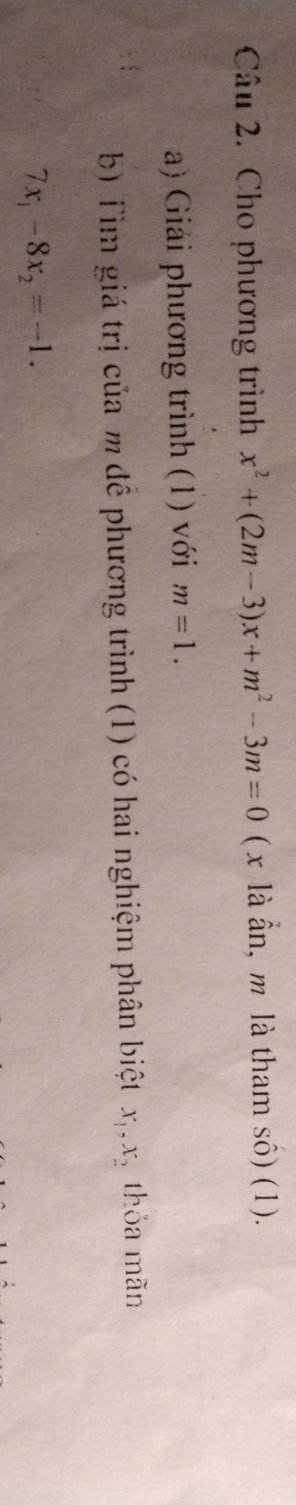\(x^2+\left(2m-3\right)x+m^2-3m=0\left(1\right)\)
a) Với x=1 thì phương trình (1) trở thành:
\(x^2-x-2=0\)
\(a=1;b=-1;c=-2\)
Ta có \(a-b+c=1-\left(-1\right)-2=0\)
Do đó phương trình trên có 2 nghiệm:
\(x_1=-1;x_2=-\dfrac{c}{a}=-\dfrac{-2}{1}=2\)
b) Để phương trình (1) có nghiệm thì:
\(\Delta\ge0\Rightarrow\left(2m-3\right)^2-4\left(m^2-3m\right)\ge0\)
\(\Leftrightarrow4m^2-12m+9-4m^2+12m\ge0\)
\(\Leftrightarrow0m^2+0m+9\ge0\) (bất phương trình vô số nghiệm).
Vậy \(\forall m\) thì phương trình (1) luôn có nghiệm.
Theo định lí Viete ta có \(\left\{{}\begin{matrix}x_1+x_2=-2m+3\\x_1x_2=m^2-3m\end{matrix}\right.\)
Ta có: \(7x_1-8x_2=-1\)
\(\Rightarrow7\left(x_1+x_2\right)+1=15x_2\) (*)
và \(8\left(x_1+x_2\right)-1=15x_1\) (**)
Nhân vế theo vế của (*) và (**) ta được:
\(\left[7\left(x_1+x_2\right)+1\right]\left[8\left(x_1+x_2\right)-1\right]=225x_1x_2\)
\(\Rightarrow\left[7\left(-2m+3\right)+1\right]\left[8\left(-2m+3\right)-1\right]=225\left(m^2-3m\right)\)
\(\Leftrightarrow\left(-14m+22\right)\left(-16m+23\right)=225m^2-675m\)
\(\Leftrightarrow224m^2-674m+506=225m^2-675m\)
\(\Leftrightarrow m^2-m-506=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=23\\m=-22\end{matrix}\right.\)
Thử lại ta có m=23 hay m=-22
a: Khi m=1 thì (1): x^2-x-2=0
=>x=2 hoặc x=-1
b:
Δ=(2m-3)^2-4(m^2-3m)
=4m^2-12m+9-4m^2+12m=9>0
=>Phương trình luôn có hai nghiệm
x1+x2=-2m+3 và 7x1-8x2=-1
=>7x1+7x2=-14m+21 và 7x1-8x2=-1
=>-x2=-14m+20 và x1+x2=-2m+3
=>x2=14m-20 và x1=-2m+3-14m+20=-16m+23
x1x2=m^2-3m
=>m^2-3m=(14m-20)(-16m+23)
=>m^2-3m=-224m^2+322m+320m-460
=>225m^2-645m+460=0
=>m=23/15 hoặc m=4/3