Câu 21: ABCD là hình bình hành
=>\(S_{ABC}=\dfrac{S_{ABCD}}{2}=\dfrac{6}{2}=3\)
=>\(\dfrac{1}{2}\cdot BA\cdot BC\cdot sinABC=3\)
=>\(\dfrac{3}{2}\cdot2\sqrt{2}\cdot sinABC=3\)
=>\(sinABC=3:3\sqrt{2}=\dfrac{1}{\sqrt{2}}\)
mà \(\widehat{ABC}>90^0\)
nên \(\widehat{ABC}=135^0\)
ABCD là hình bình hành
=>\(\widehat{ABC}+\widehat{BAD}=180^0\)
=>\(\widehat{BAD}=45^0\)
AD=BC(ABCD là hình bình hành)
mà \(BC=2\sqrt{2}\)
nên \(AD=2\sqrt{2}\)
Xét ΔABD có \(sinBAD=\dfrac{AB^2+AD^2-BD^2}{2\cdot AB\cdot AD}\)
=>\(\dfrac{3^2+\left(2\sqrt{2}\right)^2-BD^2}{2\cdot3\cdot2\sqrt{2}}=sinBAD=sin45=\dfrac{\sqrt{2}}{2}\)
=>\(17-BD^2=\dfrac{\sqrt{2}}{2}\cdot12\sqrt{2}=12\)
=>\(BD=\sqrt{17-12}=\sqrt{5}\)


 giúp mình vơiií
giúp mình vơiií











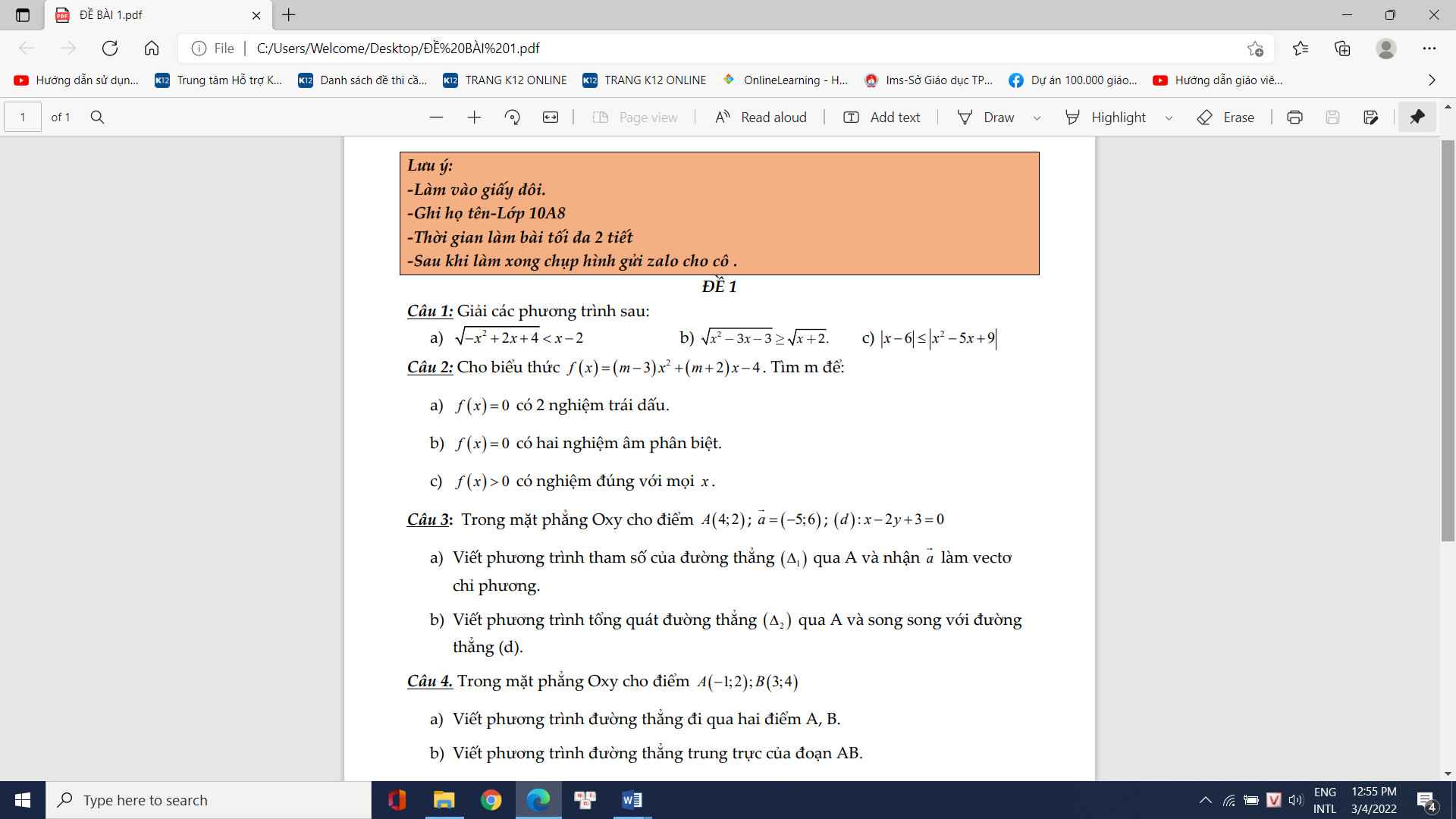

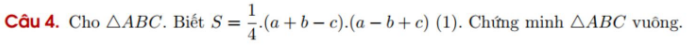


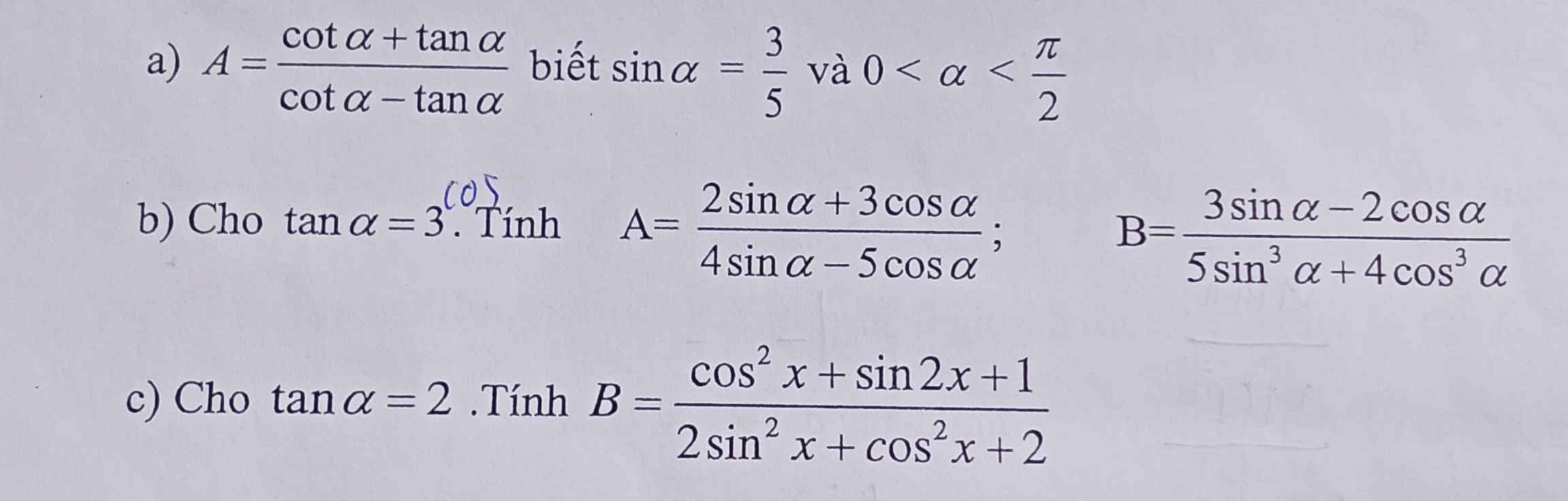



 giúp mình với giải thích cho mình luôn nhé huhu mình cảm ơn
giúp mình với giải thích cho mình luôn nhé huhu mình cảm ơn