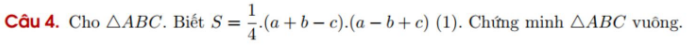Bài 1:
\(\overrightarrow{a}=\left(1;-2\right);\overrightarrow{b}=\left(2;3\right)\)
\(\overrightarrow{a}\cdot\overrightarrow{b}=1\cdot2+\left(-2\right)\cdot3=2-6=-4\)
Bài 2:
\(\overrightarrow{a}=\left(1;-2\right);\overrightarrow{b}=\left(3;4\right)\)
\(\left|\overrightarrow{a}\right|=\sqrt{1^2+\left(-2\right)^2}=\sqrt{5}\)
\(\left|\overrightarrow{b}\right|=\sqrt{3^2+4^2}=\sqrt{25}=5\)
Bài 3:
A(-1;0); B(4;-1)
\(AB=\sqrt{\left(4+1\right)^2+\left(-1-0\right)^2}\)
=>\(AB=\sqrt{5^2+1^2}=\sqrt{26}\)
Bài 4:
\(\overrightarrow{a}=\left(1;-2\right);\overrightarrow{b}=\left(3;-1\right)\)
\(\left|\overrightarrow{a}\right|=\sqrt{1^2+\left(-2\right)^2}=\sqrt{1+4}=\sqrt{5}\)
\(\left|\overrightarrow{b}\right|=\sqrt{3^2+\left(-1\right)^2}=\sqrt{9+1}=\sqrt{10}\)
\(cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}\cdot\overrightarrow{b}}{\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|}=\dfrac{1\cdot3+\left(-2\right)\cdot\left(-1\right)}{\sqrt{10}\cdot\sqrt{5}}\)
\(=\dfrac{3+2}{5\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)
=>\(\left(\overrightarrow{a},\overrightarrow{b}\right)=45^0\)
Bài 5:
\(\overrightarrow{a}=\left(1;2\right);\overrightarrow{b}=\left(2m+4;m\right)\)
Để \(\overrightarrow{a}\perp\overrightarrow{b}\) thì \(1\left(2m+4\right)+2m=0\)
=>4m+4=0
=>4m=-4
=>m=-1
Bài 6:
\(\overrightarrow{a}=\left(1;-2\right);\overrightarrow{c}=\left(3m^2-1;m\right)\)
Để \(\overrightarrow{a}\perp\overrightarrow{c}\) thì \(\overrightarrow{a}\cdot\overrightarrow{c}=0\)
=>\(1\left(3m^2-1\right)+\left(-2\right)\cdot m=0\)
=>\(3m^2-2m-1=0\)
=>\(3m^2-3m+m-1=0\)
=>(m-1)(3m+1)=0
=>\(\left[{}\begin{matrix}m-1=0\\3m+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-\dfrac{1}{3}\end{matrix}\right.\)