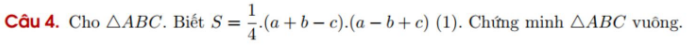2.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow sina>0\)
\(\Rightarrow sina=\sqrt{1-cos^2a}=\sqrt{1-\left(-\dfrac{1}{3}\right)^2}=\dfrac{2\sqrt{2}}{3}\)
\(sin2a=2sina.cosa=2\left(\dfrac{2\sqrt{2}}{3}\right).\left(-\dfrac{1}{3}\right)=-\dfrac{4\sqrt{2}}{9}\)
\(cos2a=2cos^2a-1=2.\left(-\dfrac{1}{3}\right)^2-1=-\dfrac{7}{9}\)
\(sin\left(a-\dfrac{\pi}{3}\right)=sina.cos\left(\dfrac{\pi}{3}\right)-cosa.sin\left(\dfrac{\pi}{3}\right)=\dfrac{2\sqrt{2}}{3}.\dfrac{1}{2}-\left(-\dfrac{1}{3}\right).\dfrac{\sqrt{3}}{2}=...\)
3.
Do \(\Delta\) có pt: \(x-3y+1=0\Rightarrow\Delta\) nhận \(\left(1;-3\right)\) là 1 vtpt
\(d\perp\Delta\Rightarrow d\) nhận \(\left(3;1\right)\) là 1 vtpt
Phương trình d có dạng:
\(3\left(x+2\right)+1\left(y-3\right)=0\Leftrightarrow3x+y+3=0\)
b.
Phương trình (C) có dạng:
\(x^2+y^2+6x+8y-11=0\)
Nên có tâm là \(I\left(-3;-4\right)\) và bán kính \(R=\sqrt{\left(-3\right)^2+\left(-4\right)^2-\left(-11\right)}=6\)