Bài 1:
a: \(\dfrac{21}{47}+\dfrac{9}{45}+\dfrac{26}{47}+\dfrac{4}{5}\)
\(=\left(\dfrac{21}{47}+\dfrac{26}{47}\right)+\left(\dfrac{1}{5}+\dfrac{4}{5}\right)\)
=1+1
=2
b:
\(\dfrac{5}{9}\cdot\dfrac{23}{11}-\dfrac{1}{11}\cdot\dfrac{5}{9}+\dfrac{5}{9}\)
\(=\dfrac{5}{9}\left(\dfrac{23}{11}-\dfrac{1}{11}+1\right)\)
\(=\dfrac{5}{9}\cdot\left(2+1\right)=\dfrac{5}{9}\cdot3=\dfrac{5}{3}\)
c: \(\dfrac{3}{4}-2\dfrac{1}{2}\cdot1,5+\dfrac{2}{5}\)
\(=\dfrac{3}{4}-\dfrac{5}{2}\cdot\dfrac{3}{2}+\dfrac{2}{5}\)
\(=\dfrac{3}{4}-\dfrac{15}{4}+\dfrac{2}{5}=-\dfrac{12}{4}+\dfrac{2}{5}=-3+\dfrac{2}{5}=-\dfrac{13}{5}\)
d: \(\dfrac{3}{7}\cdot2\dfrac{2}{3}-\dfrac{3}{7}\cdot1\dfrac{1}{2}\)
\(=\dfrac{3}{7}\left(2+\dfrac{2}{3}-1-\dfrac{1}{2}\right)\)
\(=\dfrac{3}{7}\left(1+\dfrac{2}{3}-\dfrac{1}{2}\right)=\dfrac{3}{7}\cdot\left(\dfrac{6}{6}+\dfrac{4}{6}-\dfrac{3}{6}\right)\)
\(=\dfrac{3}{7}\cdot\dfrac{7}{6}=\dfrac{3}{6}=\dfrac{1}{2}\)
e: \(\left(-0,2\right)^2\cdot5-\dfrac{2^3\cdot27^3}{4^6\cdot9^5}\)
\(=\dfrac{1}{25}\cdot5-\dfrac{2^3}{2^{12}}\cdot\dfrac{3^6}{3^{10}}=\dfrac{1}{5}-\dfrac{1}{2^9\cdot3^4}\)
\(=\dfrac{41467}{2^9\cdot3^4\cdot5}\)
f: \(57\dfrac{7}{13}:2^3+9\dfrac{7}{13}\cdot\left(-\dfrac{1}{2}\right)^3\)
\(=\left(57+\dfrac{7}{13}\right):8+\left(9+\dfrac{7}{13}\right)\cdot\dfrac{-1}{8}\)
\(=\left(57+\dfrac{7}{13}-9-\dfrac{7}{13}\right)\cdot\dfrac{1}{8}=48\cdot\dfrac{1}{8}=6\)
Bài 2:
a: \(-\dfrac{5}{12}x=\dfrac{2}{3}-\dfrac{1}{2}\)
=>\(-\dfrac{5}{12}x=\dfrac{4}{6}-\dfrac{3}{6}=\dfrac{1}{6}\)
=>\(x=\dfrac{1}{6}:\dfrac{-5}{12}=\dfrac{1}{6}\cdot\dfrac{-12}{5}=-\dfrac{2}{5}\)
b: \(\dfrac{11}{12}-\left(x+\dfrac{2}{5}\right)=\dfrac{2}{5}\)
=>\(x+\dfrac{2}{5}=\dfrac{11}{12}-\dfrac{2}{5}=\dfrac{55}{60}-\dfrac{24}{60}=\dfrac{31}{60}\)
=>\(x=\dfrac{31}{60}-\dfrac{2}{5}=\dfrac{31}{60}-\dfrac{24}{60}=\dfrac{7}{60}\)
c: \(\left|2\dfrac{1}{2}+x\right|-\dfrac{-2}{3}=3\)
=>\(\left|x+\dfrac{5}{2}\right|=3-\dfrac{2}{3}=\dfrac{7}{3}\)
=>\(\left[{}\begin{matrix}x+\dfrac{5}{2}=\dfrac{7}{3}\\x+\dfrac{5}{2}=-\dfrac{7}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}-\dfrac{5}{2}=\dfrac{14}{6}-\dfrac{15}{6}=-\dfrac{1}{6}\\x=-\dfrac{7}{3}-\dfrac{5}{2}=-\dfrac{14}{6}-\dfrac{15}{6}=-\dfrac{29}{6}\end{matrix}\right.\)
d: \(\left(2x-3\right)^2-\dfrac{3}{2}=\dfrac{19}{4}\)
=>\(\left(2x-3\right)^2=\dfrac{19}{4}+\dfrac{3}{2}=\dfrac{19}{4}+\dfrac{6}{4}=\dfrac{25}{4}\)
=>\(\left[{}\begin{matrix}2x-3=\dfrac{5}{2}\\2x-3=-\dfrac{5}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{5}{2}+3=\dfrac{11}{2}\\2x=-\dfrac{5}{2}+3=\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{11}{4}\\x=\dfrac{1}{4}\end{matrix}\right.\)
Bài `1`
\(a,\dfrac{21}{47}+\dfrac{9}{45}+\dfrac{26}{47}+\dfrac{4}{5}\)
\(=\dfrac{21}{47}+\dfrac{1}{5}+\dfrac{26}{47}+\dfrac{4}{5}\)
\(=\left(\dfrac{21}{47}+\dfrac{26}{47}\right)+\left(\dfrac{1}{5}+\dfrac{4}{5}\right)\)
\(=1+1\)
`=2`
\(b,\dfrac{5}{9}\cdot\dfrac{23}{11}-\dfrac{1}{11}\cdot\dfrac{5}{9}+\dfrac{5}{9}\)
\(=\dfrac{5}{9}\cdot\dfrac{23}{11}-\dfrac{1}{11}\cdot\dfrac{5}{9}+\dfrac{5}{9}\cdot1\)
\(=\dfrac{5}{9}\cdot\left(\dfrac{23}{11}-\dfrac{1}{11}+1\right)\)
\(=\dfrac{5}{9}\cdot3\)
\(=\dfrac{5}{3}\)
\(c,\dfrac{3}{4}-2\dfrac{1}{2}\cdot1,5+\dfrac{2}{5}\)
\(=\dfrac{3}{4}-\dfrac{5}{2}\cdot\dfrac{3}{2}+\dfrac{2}{5}\)
\(=\dfrac{3}{4}-\dfrac{15}{4}+\dfrac{2}{5}\)
\(=-3+\dfrac{2}{5}\)
\(=-\dfrac{13}{5}\)
\(d,\dfrac{3}{7}\cdot2\dfrac{2}{3}-\dfrac{3}{7}\cdot1\dfrac{1}{2}\)
\(=\dfrac{3}{7}\cdot\dfrac{8}{3}-\dfrac{3}{7}\cdot\dfrac{3}{2}\)
`= 3/7 * (8/3 - 3/2)`
`= 3/7 * 7/6`
`= 1/2`
\(e,\left(-0,2\right)^2\cdot5-\dfrac{2^3\cdot27^3}{4^6\cdot9^5}\)
\(=0,04\cdot5-\dfrac{2^3\cdot\left(3^3\right)^3}{\left(2^2\right)^6\cdot\left(3^2\right)^5}\)
\(=0,04\cdot5-\dfrac{2^3\cdot3^9}{2^{12}\cdot3^{10}}\)
\(=0,04\cdot5-\dfrac{1\cdot1}{2^9\cdot3}\)
\(=0,04\cdot5-\dfrac{1}{1536}\)
`=1/5 - 1/1536`
`= 1531/7680`
\(f,57\dfrac{7}{13}:2^3+9\dfrac{7}{13}\cdot\left(\dfrac{-1}{2}\right)^3\)
\(=\dfrac{748}{13}:8+\dfrac{124}{13}\cdot\left(\dfrac{-1}{8}\right)\)
\(=\dfrac{748}{13}\cdot\dfrac{1}{8}+\dfrac{124}{13}\cdot\left(\dfrac{-1}{8}\right)\)
\(=\dfrac{748}{13}\cdot\dfrac{1}{8}+\left(-\dfrac{124}{13}\right)\cdot\dfrac{1}{8}\)
`= [748/13 + (-124/13)] * 1/8`
`= 48 * 1/8`
`= 6`
Bài 2:
\(a,-\dfrac{5}{12}x=\dfrac{2}{3}-\dfrac{1}{2}\)
\(\dfrac{-5}{12}x=\dfrac{4}{6}-\dfrac{3}{6}\)
\(\dfrac{-5}{12}x=\dfrac{1}{6}\)
\(x=\dfrac{1}{6}:\dfrac{-5}{12}\)
\(x=\dfrac{1}{6}.\dfrac{-12}{5}\)
\(x=\dfrac{-2}{5}\)
\(b,\dfrac{11}{12}-\left(\dfrac{2}{5}+x\right)=\dfrac{2}{5}\)
\(\dfrac{2}{5}+x=\dfrac{11}{12}-\dfrac{2}{5}\)
\(\dfrac{2}{5}+x=\dfrac{55}{60}-\dfrac{24}{60}\)
\(\dfrac{2}{5}+x=\dfrac{31}{60}\)
\(x=\dfrac{31}{60}-\dfrac{2}{5}\)
\(x=\dfrac{31}{60}-\dfrac{24}{60}\)
\(x=\dfrac{7}{60}\)
\(c,\left|2\dfrac{1}{2}+x\right|-\dfrac{-2}{3}=3\)
\(\left|\dfrac{5}{2}+x\right|=3-\dfrac{2}{3}\dfrac{ }{ }\)
\(\left|\dfrac{5}{2}+x\right|=\dfrac{7}{3}\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{5}{2}+x=\dfrac{7}{3}\\\dfrac{5}{2}+x=\dfrac{-7}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{3}-\dfrac{5}{2}\\x=\dfrac{-7}{3}-\dfrac{5}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{-1}{6}\\x=\dfrac{-29}{6}\end{matrix}\right.\)
\(d,\left(2x-3\right)^2-\dfrac{3}{2}=\dfrac{19}{4}\)
\(\left(2x-3\right)^2=\dfrac{19}{4}+\dfrac{3}{2}\)
\(\left(2x-3\right)^2=\dfrac{25}{4}\)
\(\left(2x-3\right)^2=\left(\dfrac{5}{2}\right)^2\) hoặc \(\left(2x-3\right)^2=\left(\dfrac{-5}{2}\right)^2\)
\(2x-3=\dfrac{5}{2}\) hoặc \(2x-3=\dfrac{-5}{2}\)
\(2x=\dfrac{5}{2}+3\) hoặc \(2x=\dfrac{-5}{2}+3\)
\(2x=\dfrac{11}{2}\) hoặc \(2x=\dfrac{1}{2}\)
\(x=\dfrac{11}{2}:2\) hoặc \(x=\dfrac{1}{2}:2\)
\(x=\dfrac{11}{2}.\dfrac{1}{2}\) hoặc \(x=\dfrac{1}{2}.\dfrac{1}{2}\)
\(x=\dfrac{11}{4}\) hoặc \(x=\dfrac{1}{4}\)
Bài `2`
`a, -5/12x = 2/3 - 1/2`
`=> -5/12x = 1/6`
`=> x = 1/6 : -5/12`
`=> x = -2/5`
Vậy `x =-2/5`
`b, 11/12 - (2/5 + x) = 2/5`
`=> 2/5 + x = 11/12 - 2/5`
`=> 2/5 + x = 31/60`
`=> x = 31/60 - 2/5`
`=> x = 7/60`
Vậy `x = 7/60`
`c, |2 1/2 + x| - -2/3 = 3`
`=> |5/2 + x| + 2/3 = 3`
`=> |5/2 + x| = 3 - 2/3`
`=> |5/2 + x| = 7/3`
\(\Rightarrow\left[{}\begin{matrix}\dfrac{5}{2}+x=\dfrac{7}{3}\\\dfrac{5}{2}+x=-\dfrac{7}{3}\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{6}\\x=-\dfrac{29}{6}\end{matrix}\right.\)
Vậy \(x\in\left\{-\dfrac{1}{6};-\dfrac{29}{6}\right\}\)
\(d,\left(2x-3\right)^2-\dfrac{3}{2}=\dfrac{19}{4}\)
\(\Rightarrow\left(2x-3\right)^2=\dfrac{19}{4}+\dfrac{3}{2}\)
\(\Rightarrow\left(2x-3\right)^2=\dfrac{25}{4}\)
\(\Rightarrow\left(2x-3\right)^2=\left(\pm\dfrac{5}{2}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}2x-3=\dfrac{5}{2}\\2x-3=-\dfrac{5}{2}\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{11}{2}\\2x=\dfrac{1}{2}\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{11}{4}\\x=\dfrac{1}{4}\end{matrix}\right.\)
Vậy \(x\in\left\{\dfrac{11}{4};\dfrac{1}{4}\right\}\)
a) Ta có: góc A+ góc B+ góc C=ΔABC
hay 90°+ 60° + góc C= 180° ( tổng của một ∆ =180°).
⇒góc C = 180°-( 90°+ 60°)= 30°
Ta có: góc DAC + góc C + góc D=ΔDAC
hay góc DAC+ 30° + 90°= 180° ( tổng của một ∆ = 180°).
⇒góc DAC= 180°-(30°+90°)=60°
Vậy góc DAC= 60°
b)Xét ΔABI và ΔEBI, có:
BE=BA (gt)
AI= IE(Vì I là trung điểm của AE)
BI: cạnh chung
⇒ΔABI =ΔEBI (c.c.c)
⇒góc BIA= góc BIE( 2góc tương ứng)
Mà góc BIA+ góc BIE= 180° ( 2 góc kề bù)
⇒góc BIA= góc BIE= 90°
⇒AE vuông góc với BI
Mà điểm I nằm trên đường thẳng BH nên AE vuông góc với BH.
giúp mình nhanh với Ạ mình 
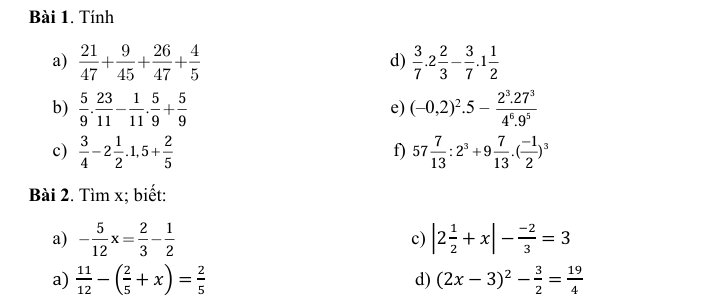
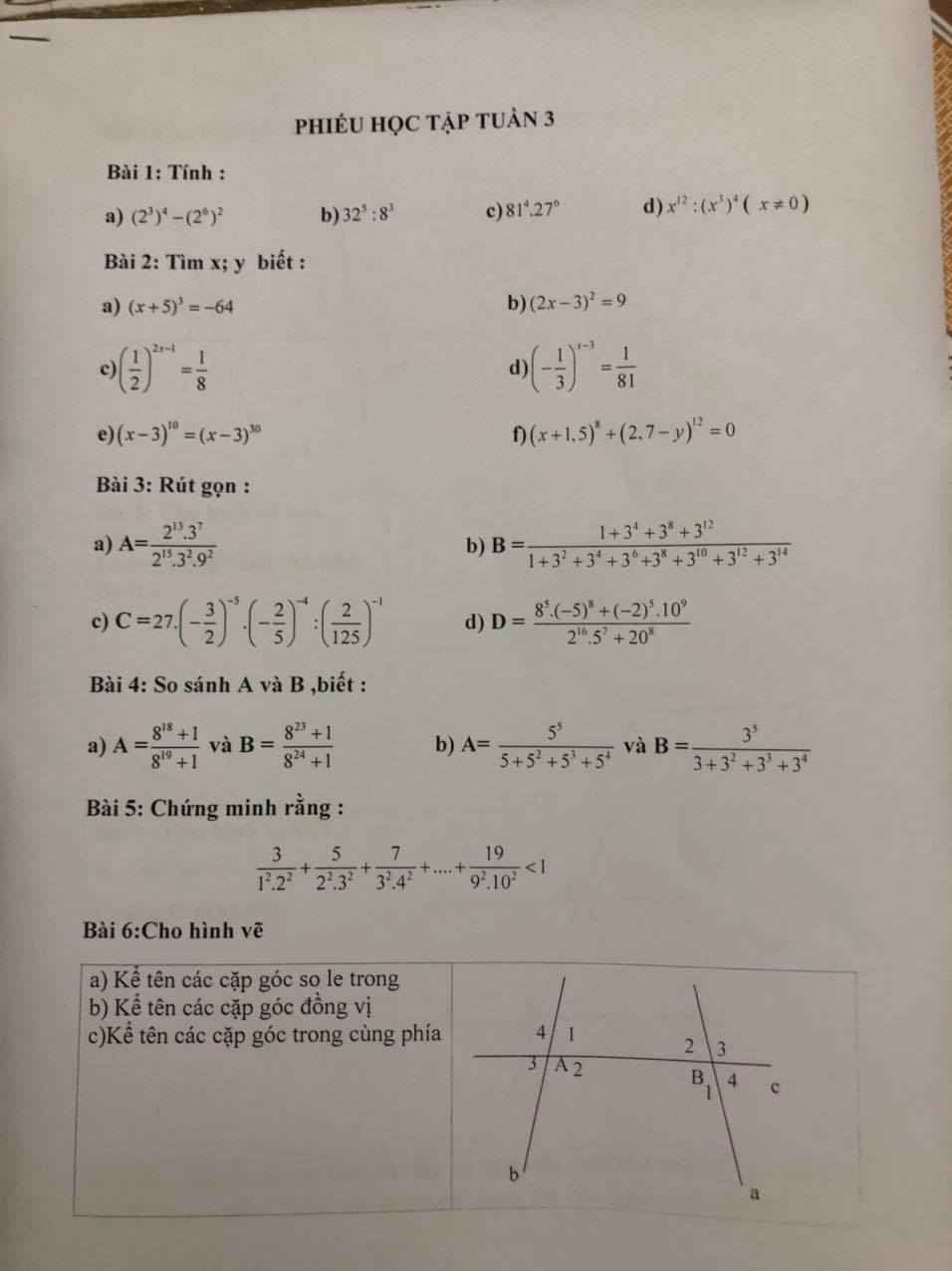nhanh giúp mình với ạ mình cảm ơn
nhanh giúp mình với ạ
nhanh giúp mình với ạ
mình đang cần gấp, gải nhanh giúp mình với ạ!!!!!
giúp mình với ạ càng nhanh càng tốt 4 câu trên ạ