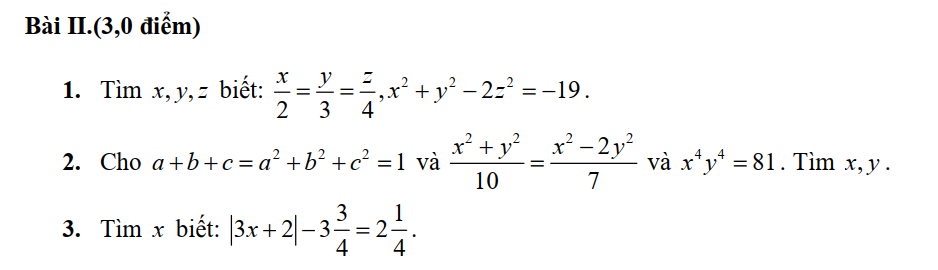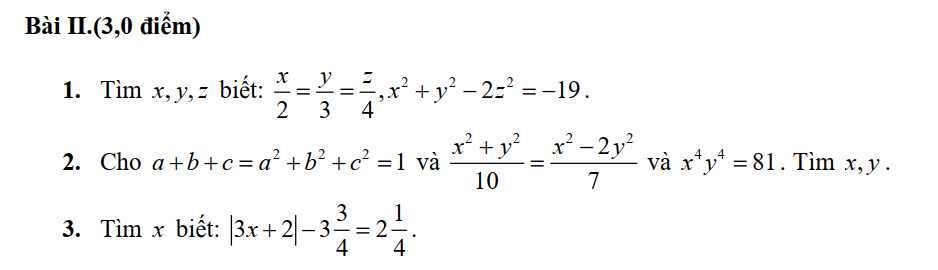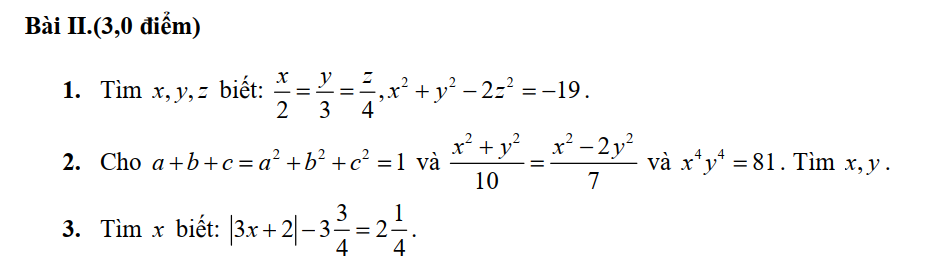1. \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\Rightarrow\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{2z^2}{32}\)
Áp dụng TCDTSBN ta có:
\(\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{2z^2}{32}=\dfrac{x^2+y^2-2z^2}{4+9-32}=\dfrac{-19}{-19}=1\)
\(\dfrac{x^2}{4}=1\Rightarrow\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\\ \dfrac{y^2}{9}=1\Rightarrow\left[{}\begin{matrix}y=-3\\y=3\end{matrix}\right.\\ \dfrac{2z^2}{32}=1\Rightarrow\left[{}\begin{matrix}z=-4\\z=4\end{matrix}\right.\)
Vậy \(\left(x,y,z\right)\in\left\{\left(-2;-3;-4\right);\left(2;3;4\right)\right\}\)