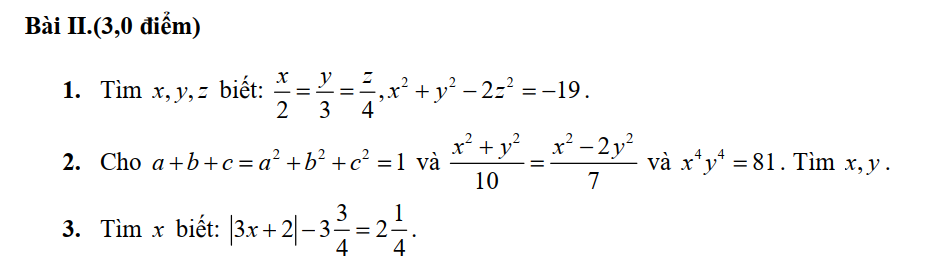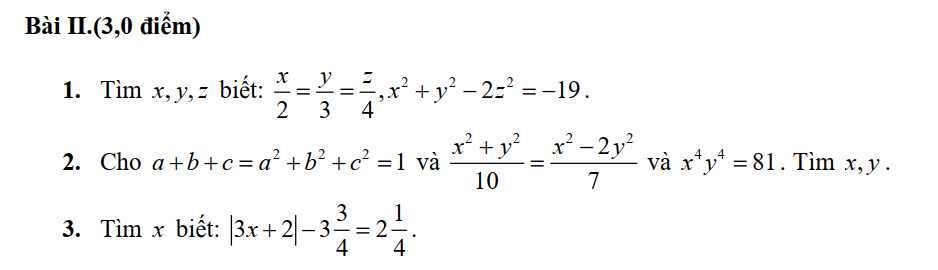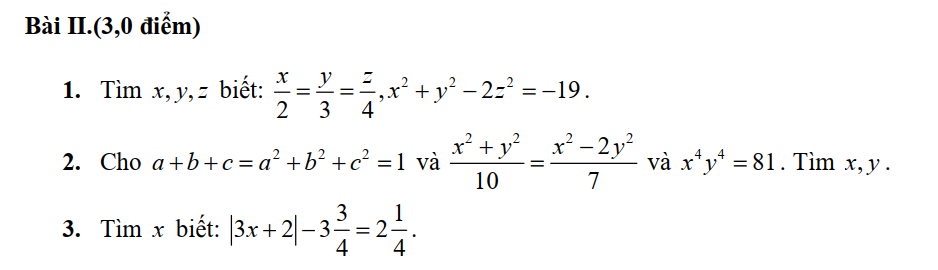\(II\\ 1,Đặt.\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=k\Leftrightarrow x=2k;y=3k;z=4k\)
Mà \(x^2+y^2-2z^2=-19\)
\(\Leftrightarrow4k^2+9k^2-32k^2=-19\\ \Leftrightarrow-19k^2=-19\Leftrightarrow k^2=1\\ \Leftrightarrow\left[{}\begin{matrix}k=1\\k=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2;y=3;z=4\\x=-2;y=-3;z=-4\end{matrix}\right.\)
\(2,\\ \dfrac{x^2+y^2}{10}=\dfrac{x^2-2y^2}{7}\Leftrightarrow7x^2+7y^2=10x^2-20y^2\\ \Leftrightarrow3x^2-27y^2=0\Leftrightarrow x^2-9y^2=0\\ \Leftrightarrow\left(x-3y\right)\left(x+3y\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3y\\x=-3y\end{matrix}\right.\)
Ta có \(x^4y^4=81\Leftrightarrow\left(xy\right)^4=3^4=\left(-3\right)^4\Leftrightarrow\left[{}\begin{matrix}xy=3\\xy=-3\end{matrix}\right.\)
Với \(x=3y\Leftrightarrow\left[{}\begin{matrix}3y^2=3\\3y^2=-3\left(vô.lí\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=1\\y=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
Với \(x=-3y\Leftrightarrow\left[{}\begin{matrix}3y^2=-3\left(vô.lí\right)\\-3y^2=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=1\\y=-1\end{matrix}\right.\left(trùng.nghiệm\right)\)
Vậy \(\left(x;y\right)=\left\{\left(3;1\right);\left(-3;-1\right)\right\}\)