Bài II:
1
a: 5x(x+3)-2(x+3)=0
=>(x+3)(5x-2)=0
=>\(\left[{}\begin{matrix}x+3=0\\5x-2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-3\\x=\dfrac{2}{5}\end{matrix}\right.\)
b: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(\dfrac{5}{x+1}+\dfrac{2}{1-x}=\dfrac{2-7x}{x^2-1}\)
=>\(\dfrac{5}{x+1}-\dfrac{2}{x-1}=\dfrac{-7x+2}{\left(x-1\right)\left(x+1\right)}\)
=>\(\dfrac{5\left(x-1\right)-2\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{-7x+2}{\left(x-1\right)\left(x+1\right)}\)
=>5x-5-2x-2=-7x+2
=>3x-7=-7x+2
=>10x=9
=>x=9/10(nhận)
2:
\(\dfrac{1}{4}\left(x-3\right)< =2x+3\)
=>\(\dfrac{1}{4}x-\dfrac{3}{4}< =2x+3\)
=>\(\dfrac{1}{4}x-2x< =3+\dfrac{3}{4}\)
=>\(-\dfrac{7}{4}x< =\dfrac{12}{4}+\dfrac{3}{4}=\dfrac{15}{4}\)
=>-7x<=15
=>\(x>=-\dfrac{15}{7}\)
Bài III:
1: Gọi thời gian vòi I và vòi II chảy một mình đầy bể lần lượt là x(giờ) và y(giờ)
(Điều kiện: x>0; y>0)
Trong 1 giờ, vòi I chảy được: \(\dfrac{1}{x}\left(bể\right)\)
Trong 1 giờ, vòi II chảy được: \(\dfrac{1}{y}\left(bể\right)\)
Trong 1 giờ, hai vòi chảy được: \(\dfrac{1}{6}\left(bể\right)\)
Do đó: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\left(1\right)\)
Trong 2 giờ, vòi I chảy được: \(2\cdot\dfrac{1}{x}=\dfrac{2}{x}\left(bể\right)\)
Trong 3 giờ, vòi II chảy được: \(3\cdot\dfrac{1}{y}=\dfrac{3}{y}\left(bể\right)\)
Nếu vòi I chảy trong 2 giờ và vòi II chảy trong 3 giờ thì hai vòi chảy được 2/5 bể nên \(\dfrac{2}{x}+\dfrac{3}{y}=\dfrac{2}{5}\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{2}{x}+\dfrac{3}{y}=\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=\dfrac{2}{6}=\dfrac{1}{3}\\\dfrac{2}{x}+\dfrac{3}{y}=\dfrac{2}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y}-\dfrac{2}{x}-\dfrac{2}{y}=\dfrac{2}{5}-\dfrac{1}{3}=\dfrac{1}{15}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1}{15}\\\dfrac{1}{x}=\dfrac{1}{6}-\dfrac{1}{15}=\dfrac{5}{30}-\dfrac{2}{30}=\dfrac{3}{30}=\dfrac{1}{10}\end{matrix}\right.\)
=>y=15(nhận); x=10(nhận)
Vậy: thời gian vòi I và vòi II chảy một mình đầy bể lần lượt là 10(giờ) và 15(giờ)
2: Gọi độ dài quãng đường từ Thanh Hóa ra Hà Nội là x(km)
(Điều kiện: x>0)
Thời gian đi là \(\dfrac{x}{42}\left(giờ\right)\)
Thời gian về là \(\dfrac{x}{36}\left(giờ\right)\)
Thời gian về nhiều hơn thời gian đi là 45p=0,75 giờ nên ta có:
\(\dfrac{x}{36}-\dfrac{x}{42}=0,75\)
=>\(\dfrac{7x}{252}-\dfrac{6x}{252}=0,75\)
=>\(\dfrac{x}{252}=0,75\)
=>\(x=252\cdot0,75=189\left(nhận\right)\)
Vậy: Độ dài quãng đường từ Thanh Hóa ra Hà Nội dài 189km
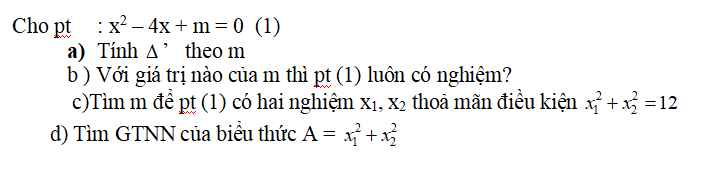giúp mình với ạ.Mình cần lời giải chi tiết
).
