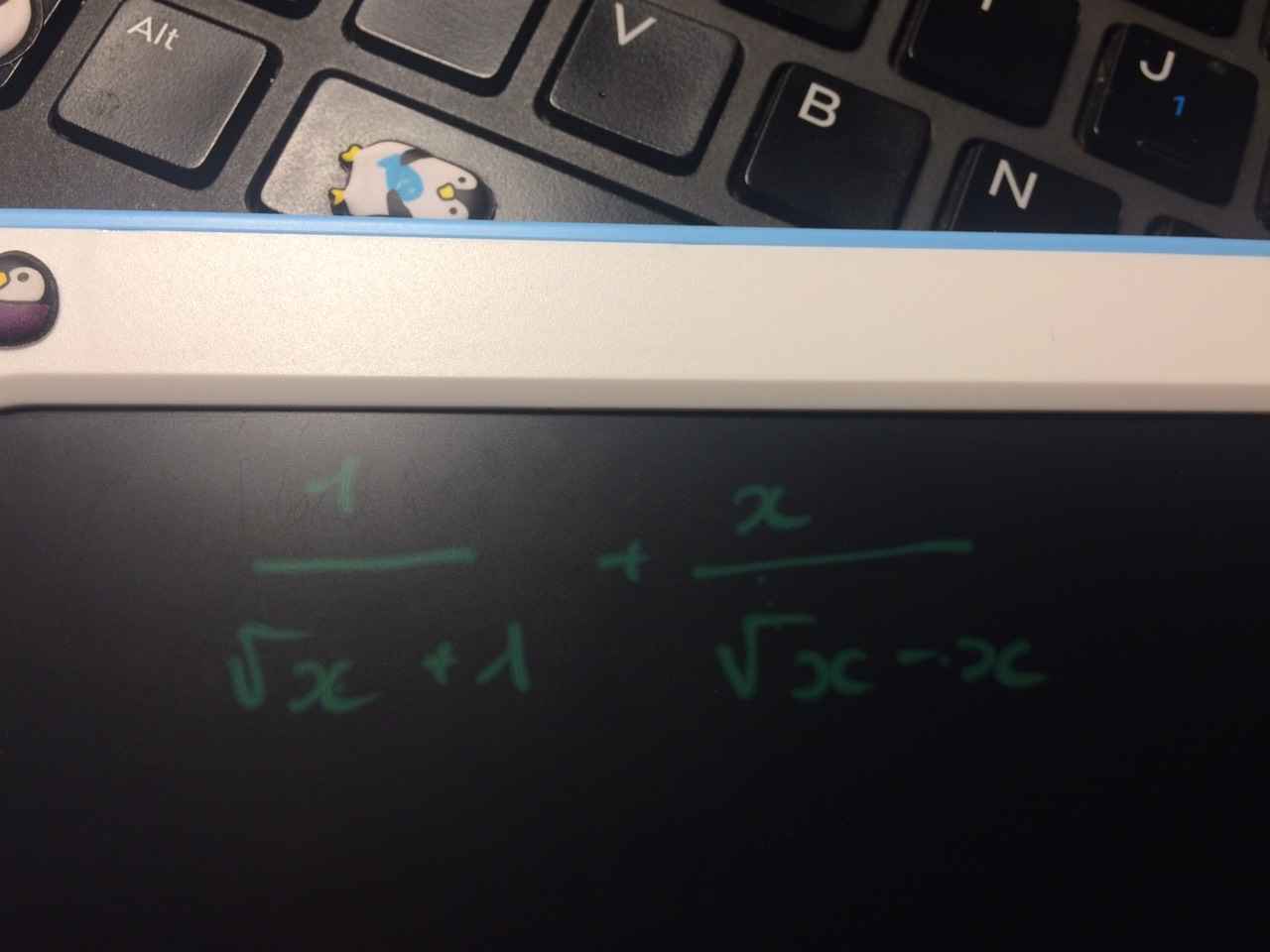1.\(x=4-2\sqrt{3}-\left(\sqrt{3}\right)^2-2.\sqrt{3}.1+1^2=\left(\sqrt{3}-1\right)^2\)
\(A=\dfrac{2x-3\sqrt{x}-2}{\sqrt{x}-2}=\dfrac{\left(\sqrt{x}-2\right)\left(2\sqrt{x}+1\right)}{\sqrt{x}-2}=2\sqrt{x}+1=2\sqrt{\left(\sqrt{3}-1\right)^2}+1=2\left(\sqrt{3}-1\right)+1=2\sqrt{3}-2+1=2\sqrt{3}-1\)
2.\(B=\dfrac{\sqrt{x^3}-\sqrt{x}+2x-2}{\sqrt{x}+2}=\dfrac{\sqrt{x}^2\left(\sqrt{x}+2\right)-\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)}=\dfrac{\left(\sqrt{x}+2\right)\left(x-1\right)}{\sqrt{x}+2}=x-1\)
\(B=A+1\)
\(\Leftrightarrow x-1=2\sqrt{x}+1+1\)
\(\Leftrightarrow x-1=2\sqrt{x}+2\)
\(\Leftrightarrow x-2x\sqrt{x}-3=0\)
\(\Leftrightarrow\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=3\\\sqrt{x}=-1\left(vô.lý\right)\end{matrix}\right.\) \(\rightarrow x=\sqrt{3}\)






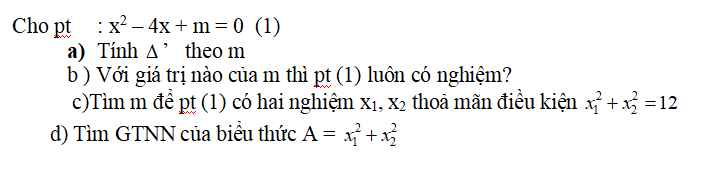 giúp mình với ạ.Mình cần lời giải chi tiết
giúp mình với ạ.Mình cần lời giải chi tiết