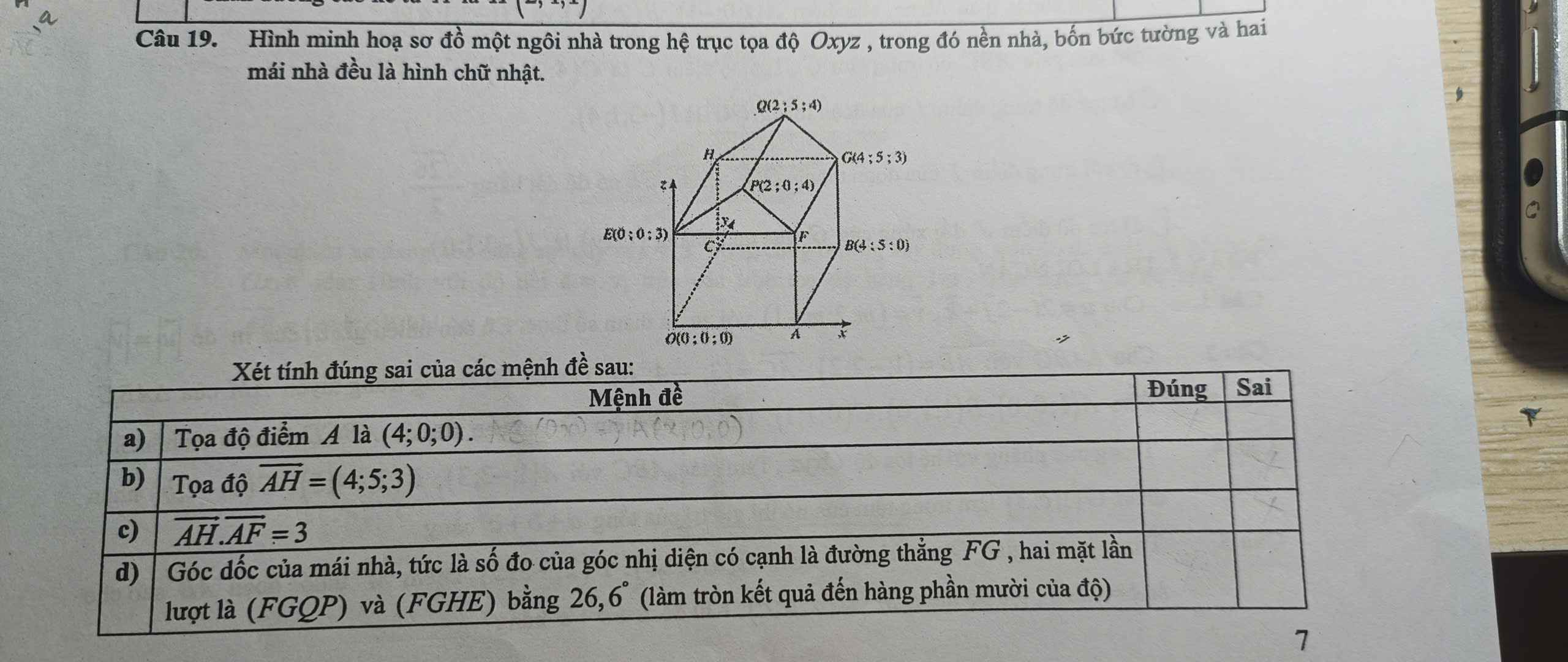
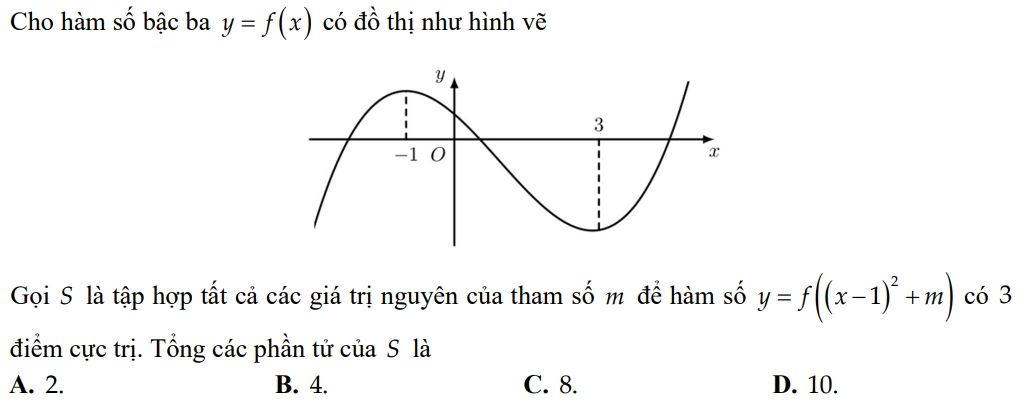
a) Đúng
b) \(A\left(4;0;0\right)\)
\(H\left(0;5;3\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(-4;5;3\right)\)
\(\Rightarrow\) Sai
c) \(F\left(4;0;3\right)\Rightarrow\overrightarrow{AF}=\left(0;0;3\right)\)
\(\overrightarrow{AH}.\overrightarrow{AF}=-4.0+5.0+3.3=9\)
\(\Rightarrow\) Sai
d) \(\overrightarrow{FP}=\left(-2;0;1\right);\overrightarrow{FE}=\left(-4;0;0\right)\)
Góc nhị diện của \(\left(FGQP\right)\&\left(FGHE\right)\) là góc của 2 vec tơ \(\overrightarrow{FP}\&\overrightarrow{FE}\)
\(cos\left(\widehat{\overrightarrow{FP};\overrightarrow{FE}}\right)=\dfrac{-2.\left(-4\right)+0.0+1.0}{\sqrt{4+1}.\sqrt{16}}=0,895\Rightarrow\left(\widehat{\overrightarrow{FP};\overrightarrow{FE}}\right)=26,6^o\)
\(\Rightarrow\) Đúng
a) Đúng
- Giải thích:
`A in Ox => y_A = 0` và `y_A = 0`
Mà `B (4;5;0)` và `AB` // `OC => x_A = 4`
b) Sai
`H(0;5;3) `
`=> vec{AH} = (0-4;5-0;3-0) = (-4;5;3)`