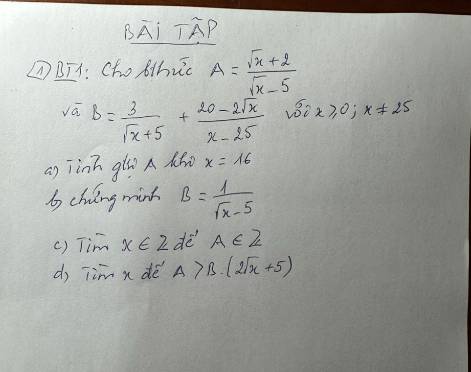a) Ta có:
\(\widehat{MIC}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\widehat{MEC}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow\) tứ giác \(EMCI\) có hai góc đối nhau bằng \(90^o\) nên nội tiếp đường tròn
b) Xét \(ΔDEB\) và \(ΔDMC\), ta có:
\(\widehat{EDB}=\widehat{MDC}\left(đối.đỉnh\right)\)
\(\widehat{DBE}=\widehat{DMC}\) (cùng chắn cung \(MB\))
\(\RightarrowΔDEB ~ ΔDMC (g.g)\)
\(\Rightarrow\dfrac{DE}{DM}=\dfrac{DB}{DC}\)
mà \(DC=2R\)
\(\Rightarrow DE.DM=DB.DC=DB.2R\)
\(\Rightarrow DE.DM=DB^2\)
c) Gọi \(H\) là trung điểm của \(EK\)
Xét \(ΔMEK\), ta có:
\(MH\) là đường trung tuyến (\(H\) là trung điểm \(EK\))
mà \(MI\perp EK\) (\(MI\) là đường cao trong tam giác vuông \(EMC\))
\(\Rightarrow\) \(MH\) là đường trung trực của \(EK\)
\(\Rightarrow\) \(MH\perp OM\) tại \(H\)
mà \(MH\) đi qua \(M\)
\(\Rightarrow\) \(MH\) là tiếp tuyến của đường tròn \(\left(O\right)\) tại \(M\)
d) Xét \(ΔBEI\) và \(ΔBKA\), ta có:
\(\widehat{BIE}=\widehat{BKA}\) (cùng chắn cung \(BI\))
\(\widehat{EBI}=\widehat{KAB}\) (cùng chắn cung \(MB\))
\(\RightarrowΔBEI ~ ΔBKA (g.g)\)
\(\Rightarrow\dfrac{BE}{BK}=\dfrac{IE}{IA}\left(đpcm\right)\)