a) Xét tam giác \(ABD\) có :
\(\widehat{DAB}=90^o\left(HCN\right)\)
\(AD=BC=a\)
\(AB=a\sqrt{3}\)
\(\Rightarrow\Delta ABD\) là tam giác nửa đều
\(\Rightarrow\widehat{ABD}=30^o\)
b) Xét tam giác vuông \(DCE\)
\(AE=\dfrac{2}{3}AD\Rightarrow ED=\dfrac{1}{3}AD=\dfrac{a}{3}\)
\(CD=AB=a\sqrt{3}\left(HCN\right)\)
\(CE^2=ED^2+CD^2=\dfrac{a^2}{9}+3a^2=\dfrac{28a^2}{9}\left(Pitago\right)\)
\(\Rightarrow CE=\dfrac{2a\sqrt{7}}{3}\)
\(sin\widehat{ECD}=cos\widehat{DEC}=\dfrac{ED}{CE}=\dfrac{\dfrac{a}{3}}{\dfrac{2a\sqrt{7}}{3}}=\dfrac{1}{2\sqrt{7}}\)
\(cos\widehat{ECD}=sin\widehat{DEC}=\dfrac{CD}{CE}=\dfrac{a\sqrt{3}}{\dfrac{2a\sqrt{7}}{3}}=\dfrac{3\sqrt{3}}{2\sqrt{7}}\)
\(tan\widehat{ECD}=cot\widehat{DEC}=\dfrac{sin\widehat{ECD}}{cos\widehat{ECD}}=\dfrac{\dfrac{1}{2\sqrt{7}}}{\dfrac{3\sqrt{3}}{2\sqrt{7}}}=\dfrac{1}{3\sqrt{3}}\)
\(cot\widehat{ECD}=tan\widehat{DEC}=\dfrac{1}{tan\widehat{ECD}}=3\sqrt{3}\)
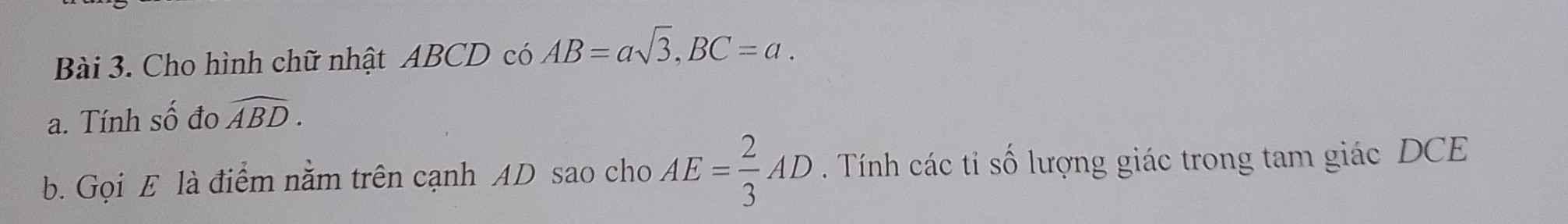
giúp mình câu b) c) với ạ
giúp mình mấy câu này với mình cảm ơn nhìu ạ