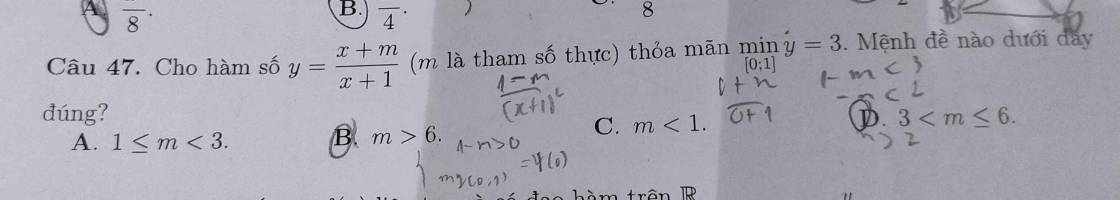Lời giải:
Bài toán tương đương với:
Tìm $m\in [-10;10]$ để $f(x)=(m+2)x^2-x+3m^2-2m$ với $x\in [0;+\infty)$ có GTLN.
Với $m=-2$ thì $f(x)=-x+16\leq 16$ với mọi $x\geq 0$ nên đạt gtln =16 tại $x=0$
Với $m>-2$ thì $f(x)$ là hàm bậc 2 có hệ số cao nhất dương. Đồng thời $x$ không bị chặn trên nên $f(x)$ không có gtln.
Với $m< -2$ thì $f'(x)=2x(m+2)-1<0$ với mọi $x\geq 0$
$\Rightarrow f(x)$ nghịch biến trên $[0;+\infty)$
$\Rightarrow f(x)\leq f(0)$ tức là hàm số có gtln.
Vậy $m\leq -2$. Tức là $m$ có thể nhận các giá trị $-2, -3, -4, -5, -6, -7, -8, -9,-10$, hay có 9 giá trị $m$ thỏa mãn.