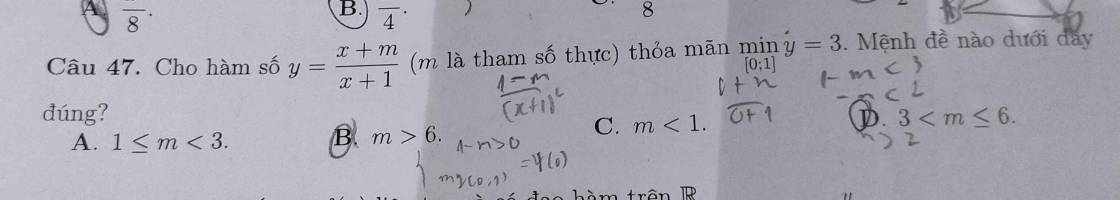Lời giải:
\(y'=\frac{1-m}{(x+1)^2}\)
Nếu $m=1$ thì $y=1$ với mọi $x\neq -1$ (loại)
Nếu $m> 1$ thì hàm số nghịch biến trên TXĐ
$\Rightarrow$ với $x\in [0;1]$ thì:
$y_{\min}=y(1)=\frac{m+1}{2}=3$
$\Leftrightarrow m=5$
Nếu $m<1$ thì hàm số đồng biến trên TXĐ
$\Rightarrow$ với $x\in [0;1]$ thì:
$y_{\min}=y(0)=\frac{0+m}{0+1}=3\Leftrightarrow m=3$ (vô lý do $m< 1$)
Vậy $m=5$. Nghĩa là đáp án D đúng.
Đúng 1
Bình luận (0)