Làm biếng tính tích có hướng nên biến đổi đại số thuần túy:
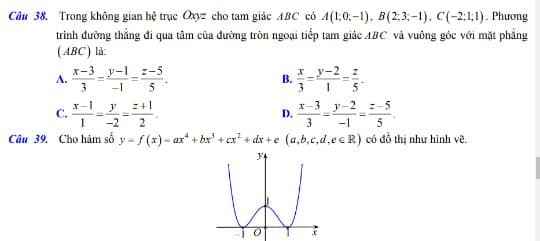
Gọi \(M\left(x;y;z\right)\) là điểm bất kì thuộc đường thẳng cần tìm
\(\Rightarrow MA=MB=MC\)
\(\Rightarrow\left\{{}\begin{matrix}\left|\overrightarrow{MA}\right|=\left|\overrightarrow{MB}\right|\\\left|\overrightarrow{MB}\right|=\left|\overrightarrow{MC}\right|\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-1\right)^2+y^2+\left(z+1\right)^2=\left(x-2\right)^2+\left(y-3\right)^2+\left(z+1\right)^2\\\left(x-2\right)^2+\left(y-3\right)^2+\left(z+1\right)^2=\left(x+2\right)^2+\left(y-1\right)^2+\left(z-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+3y-6=0\\2x+y-z-2=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+3y-6=0\\5y+z-10=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=-3\left(y-1\right)\\5\left(y-1\right)=-\left(z-5\right)\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x-3}{3}=\dfrac{y-1}{-1}\\\dfrac{y-1}{-1}=\dfrac{z-5}{5}\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{x-3}{3}=\dfrac{y-1}{-1}=\dfrac{z-5}{5}\)