kẻ đường cao AH (H thuộc BC)
trong △ ABC có: góc A + góc B + góc C = 180 độ
⇒ góc A = 180 độ - góc B - góc C
góc A = 180 độ - 20 độ - 30 độ = 130 độ
trong △ ABH vuông tại H có: \(AH=AB\cdot\sin B=AB\cdot\sin20^0\)
trong △ ACH vuông tại H có: \(AH=AC\cdot\sin C=AC\cdot\sin30^0\)
theo định lý sin ta có:
\(\frac{BC}{\sin A}=\frac{AC}{\sin B}\Rightarrow AC=\frac{BC\cdot\sin B}{\sin A}=\frac{60\cdot\sin20^0}{\sin130^0}\)
\(AH=AC\cdot\sin30^0=\frac{60\cdot\sin20^0}{\sin130^0}\cdot\sin30^0\left(\operatorname{cm}\right)\)
diện tích hình △ ABC là:
\(\frac{AH\cdot BC}{2}=\frac{\frac{60\cdot\sin20^0}{\sin130^0}\cdot\sin30^0\cdot60}{2}\approx401,828\left(\operatorname{cm}^2\right)\)





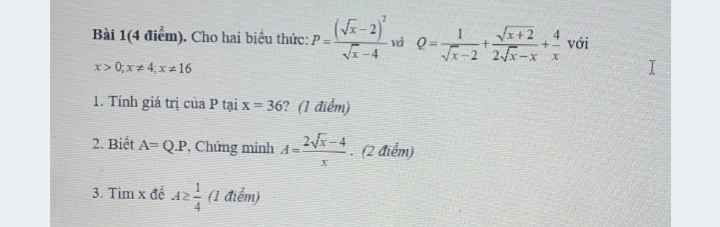





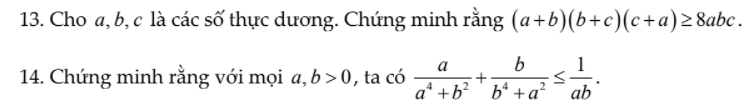

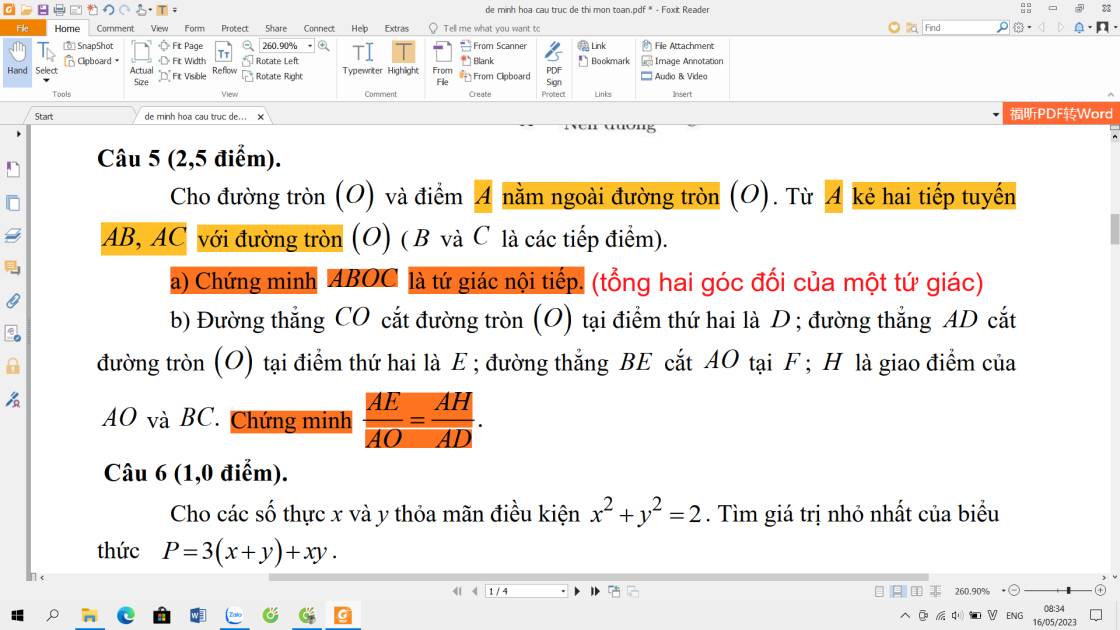 giải giúp mình 2 câu này với ạ
giải giúp mình 2 câu này với ạ








