a. Xét 2 tam giác vuông: BME và CMF có:
\(\left\{{}\begin{matrix}\widehat{BME}=\widehat{CMF}\left(đối.đỉnh\right)\\BM=MC\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta BME=\Delta CMF\left(c.h-g.n\right)\)
\(\Rightarrow CF=BE\) (1)
Ta có: BE // CF (cùng vuông góc với AM) (2)
Từ (1) và (2), suy ra: tứ giác FCEB là HBH.
\(\Rightarrow\) BF // CE
a, Xét \(\Delta BEM.và.\Delta CFM:\)
\(\widehat{BEM}=\widehat{CFM}=90^0\\ BM=CM\\ \widehat{BME}=\widehat{CMF}\left(đối.đỉnh\right)\\ \Rightarrow\Delta...=\Delta....\left(ch,gn\right)\\ \Rightarrow EM=FM\\ Xét.\Delta BMF.và.\Delta CME.có:\\ BM=CM\\ \widehat{BMF}=\widehat{CME}\\ MF=ME\\ \Rightarrow\Delta....=\Delta...\left(c.g.c\right)\\ \Rightarrow\widehat{MBF}=\widehat{MCE}\\ Mà.2.góc.so.le.trong\)
--> BE//CE
\(b,AE+Em=AM\\ AF-MF=AM\\ \Rightarrow AE+AF+EM-MF=2AM\\ màEM=MF\\ \Rightarrow EM=MF\Rightarrow EM+AF=2AM\\ AM=\dfrac{AE+AF}{2}\)
\(c,Vì\Delta ABE.vuông,tại,E\\ \Rightarrow AE< AB\\ \Delta AFC.vuông.ở.F\\ \Rightarrow AF< AC\\ \Rightarrow AE+AF< AB+AC\\ \Rightarrow\dfrac{AB+AF}{2}< \dfrac{AB+AC}{2}\\ \Rightarrow AM< \dfrac{AB+AC}{2}\)
b/AE+AF=AM-EM+AM+MF.
mà EM=MF (△BME=△CMF).
=>AE+AF=AM+AM=2AM.
c/ Tâ có: AE+AF=2AM nên \(AM=\dfrac{AE+AF}{2}\).
Mà \(AB>AE\) (quan hệ giữa đường vuông góc và đường xiên).
\(AC>AF\)(quan hệ giữa đường vuông góc và đường xiên).
=>\(AM< \dfrac{AB+AC}{2}\)
Bài 5:
\(\sqrt{\left(x-\sqrt{2}\right)^2}+\sqrt{\left(x-z+\sqrt{2}\right)^2}+\left|x-y+z\right|=0\)
Do \(\sqrt{\left(x-\sqrt{2}\right)^2}\ge0;\sqrt{\left(x-z+\sqrt{2}\right)^2}\ge0;\left|x-y+z\right|\ge0\)
=>\(\sqrt{\left(x-\sqrt{2}\right)^2}=0;\sqrt{\left(x-z+\sqrt{2}\right)^2}=0;\left|x-y+z\right|=0\)
=>\(\left(x-\sqrt{2}\right)^2=0;\left(x-z+\sqrt{2}\right)^2=0;x-y+z=0\)
=>\(x-\sqrt{2}=0;x-z+\sqrt{2}=0;x-y+z=0\)
=>\(x=\sqrt{2};x-z+\sqrt{2}=0;x-y+z=0\)
=>\(x=\sqrt{2};\sqrt{2}-z+\sqrt{2}=0;x-y+z=0\)
=>\(x=\sqrt{2};z=2\sqrt{2};x-y+z=0\)
=>\(x=\sqrt{2};z=2\sqrt{2};\sqrt{2}-y+2\sqrt{2}=0\)
=>\(x=\sqrt{2};z=2\sqrt{2};y=3\sqrt{2}\)



















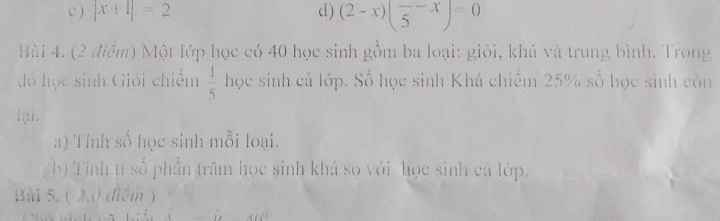

 giúp mình bài 4 với
giúp mình bài 4 với