Câu 5:
Tại t = 0 vật có li độ x0 > 0 và đang giảm, nên vật đi theo chiều âm.
Từ thời điểm t1 = 0,2s đến t2 = 0,3s, góc quét được: \(\omega.\left(t_2-t_3\right)=\dfrac{2\pi}{1,6}.\left(0,3-0,2\right)=\dfrac{\pi}{8}\) (rad)
⇒ \(\alpha_1=\dfrac{\pi}{2}-\dfrac{\pi}{8}=\dfrac{3\pi}{8}\) (rad)
Tại thời điểm t1 = 0,2s vật có li độ x = 2cm ⇒ \(A.cos\dfrac{3\pi}{8}=2\Rightarrow A=\dfrac{2}{cos\dfrac{3\pi}{8}}\left(cm\right)\)
Từ thời điểm t2 = 0,3s đến t3 = 0,9s, góc quét được:
\(\omega.\left(t_3-t_2\right)=\dfrac{2\pi}{1,6}.\left(0,9-0,3\right)=\dfrac{3\pi}{4}\) (rad)
\(\Rightarrow\alpha_2=\dfrac{3\pi}{4}-\dfrac{\pi}{2}=\dfrac{\pi}{4}\) (rad)
Tại thời điểm t3 = 0,9s, vật có li độ \(x=-A.cos\left(\dfrac{\pi}{4}\right)=-\dfrac{2}{cos\dfrac{3\pi}{8}}.\dfrac{\sqrt{2}}{2}=-\dfrac{\sqrt{2}}{cos\dfrac{3\pi}{8}}\left(cm\right)\)
Giá trị của gia tốc tại thời điểm t3 = 0,9s là: \(a=-\omega^2.x=-\left(\dfrac{2\pi}{1,6}\right)^2.-\dfrac{\sqrt{2}}{cos\dfrac{3\pi}{8}}\approx57\)cm/s2
Đúng 3
Bình luận (1)
Các câu hỏi tương tự
Mọi người ơi giúp mình 2 câu này với ạ. Mình cảm ơn mọi người rất nhiều ạ 
Các bạn giúp mình 2 câu TL này với ạ!!
Giúp em câu này với ạ em đang cần gấp.em cảm ơn ạ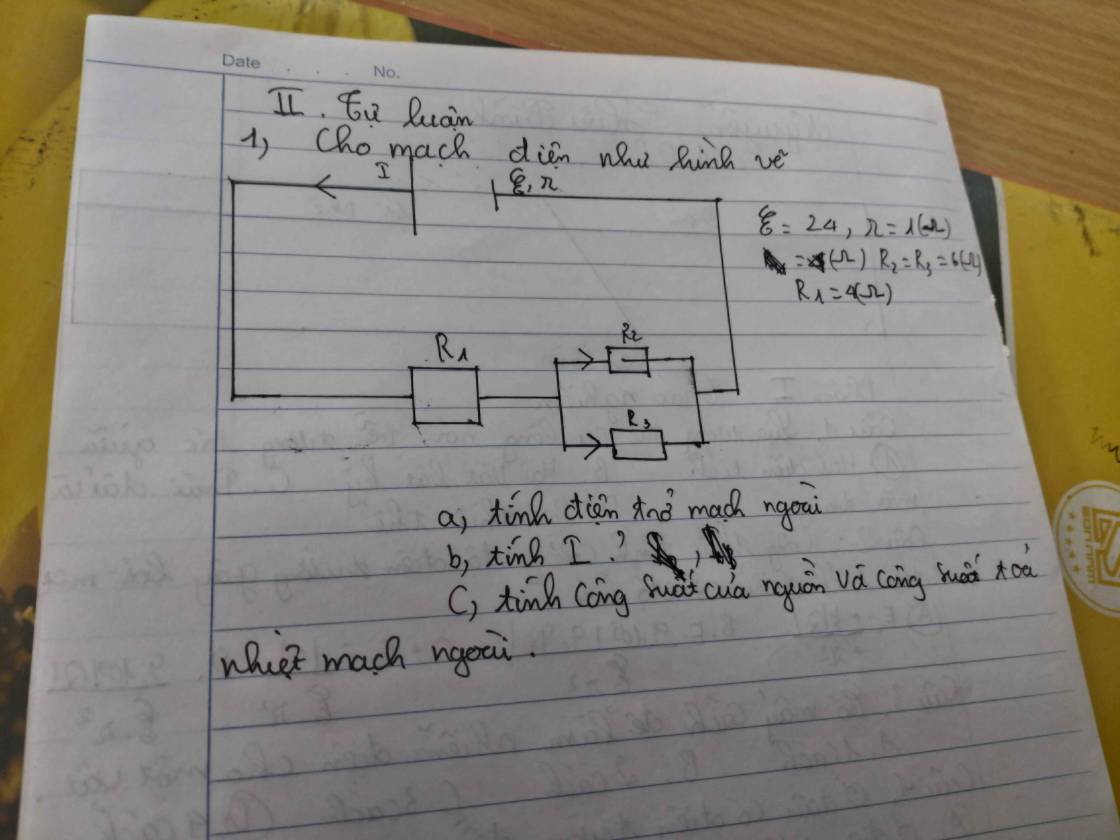
Dạ mọi người giúp em câu này với ạ

Mọi người giúp em giải câu này với ạ. Em cảm ơn
Giúp mình câu 10d với ạ

mình cần giải gấp câu vật lý này ạ cảm ơn mng ạ
 Các bạn giúp mình câu c ạ, mình cảm ơn
Các bạn giúp mình câu c ạ, mình cảm ơn
Giải giúp mình bài 2 với ạ 
Giúp em bài này với ạ















