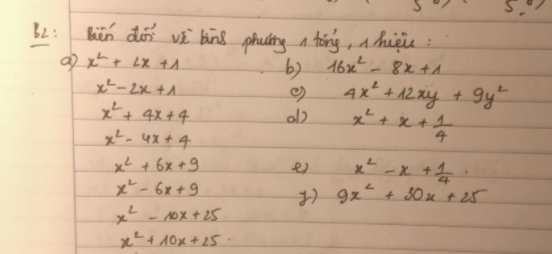a) \(x^2+2x+1=\left(x+1\right)^2\)
\(x^2-2x+1=\left(x-1\right)^2\)
\(x^2+4x+4=\left(x+2\right)^2\)
\(x^2-4x+4=\left(x-2\right)^2\)
\(x^2+6x+9=\left(x+3\right)^2\)
\(x^2-6x+9=\left(x-3\right)^2\)
\(x^2-10x+25=\left(x-5\right)^2\)
\(x^2+10x+25=\left(x+5\right)^2\)
b) \(16x^2-8x+1=\left(4x-1\right)^2\)
c) \(4x^2+12xy+9y^2=\left(2x+3y\right)^2\)
d) \(x^2+x+\dfrac{1}{4}=\left(x+\dfrac{1}{2}\right)^2\)
e) \(x^2-x+\dfrac{1}{4}=\left(x-\dfrac{1}{2}\right)^2\)
f) \(9x^2+30x+25=\left(3x+5\right)^2\)
a=\(\left(x+1\right)^2\)
=\(\left(x-1\right)^2\)
=\(\left(x+2\right)^2\)
=\(\left(x-2\right)^2\)
=\(\left(x+3\right)^2\)
=\(\left(x-3\right)^2\)
=\(\left(x-5\right)^2\)
=\(\left(x+5\right)^2\)
b, =\(\left( 4 𝑥 − 1\right)^2\)
c,=\(\left(2x-3y\right)^2\)
a: \(x^2+2x+1=\left(x+1\right)^2\)
\(x^2-2x+1=\left(x-1\right)^2\)
\(x^2+4x+4=\left(x+2\right)^2\)
\(x^2-4x+4=\left(x-2\right)^2\)
\(x^2+6x+9=\left(x+3\right)^2\)
\(x^2-6x+9=\left(x-3\right)^2\)
\(x^2-10x+25=\left(x-5\right)^2\)
\(x^2+10x+25=\left(x+5\right)^2\)
b: \(16x^2-8x+1=\left(4x-1\right)^2\)
c: \(4x^2+12xy+9y^2=\left(2x+3y\right)^2\)
d: \(x^2+x+\dfrac{1}{4}=\left(x+\dfrac{1}{2}\right)^2\)
e: \(x^2-x+\dfrac{1}{4}=\left(x-\dfrac{1}{2}\right)^2\)