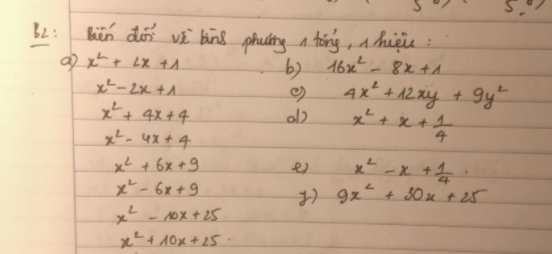1/ Xét \(\Delta ABC\) và \(\Delta HAC\) có:
∠A = ∠AHC = 90 độ
∠C là góc chung
Do đó: △ABC ∼ △HAC (g . g)
2/ Ta có: \(\Delta HAC\sim\Delta ABC\)
\(\Rightarrow\dfrac{AC}{HC}=\dfrac{BC}{AC}\)
\(\Rightarrow AC.AC=HC.BC\)
\(\Rightarrow AC^2=HC.BC\) (đpcm)
3/ Đặt BD là x, theo tính chất đường phân giác, ta có:
\(\dfrac{AB}{AC}=\dfrac{BD}{DC}\Rightarrow\dfrac{9}{12}=\dfrac{x}{15-x}\)
\(\Rightarrow9\left(15-x\right)=12x\)
\(\Rightarrow135-9x=12x\)
\(\Rightarrow135=12x+9x\)
\(\Rightarrow135=21x\)
\(\Rightarrow x\approx6,4\)
Độ dài của DC là: \(15-x\Rightarrow15-6,4=8,6\)
Vậy BD = 6,4 cm và DC = 8,6 cm

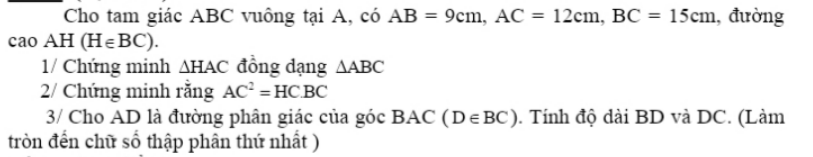









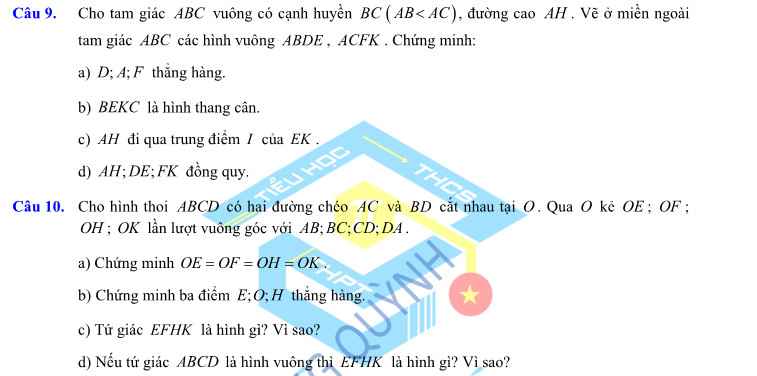
 Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều
Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều