f(x) xác định \(< =>1-x-2x^2\ge0\)
\(< =>-2x^2-x+1\ge0\)
\(< =>-2\left(x^2+\dfrac{1}{2}x-\dfrac{1}{2}\right)\ge0\)
\(< =>-2\left(x^2+2.\dfrac{1}{4}x+\dfrac{1}{16}-\dfrac{9}{16}\right)\ge0\)
\(< =>-2\left[\left(x+\dfrac{1}{4}-\dfrac{3}{4}\right)\left(x+\dfrac{1}{4}+\dfrac{3}{4}\right)\right]\ge0\)
\(=>-2\left(x-\dfrac{1}{2}\right)\left(x+1\right)\ge0\)
\(< =>-\left(x+1\right)\left(2x-1\right)\ge0\)
\(< =>-\left(x+1\right)\left(2x-1\right)\ge0\)
\(=>\left[{}\begin{matrix}\left\{{}\begin{matrix}-\left(x+1\right)\ge0\\2x-1\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}-\left(x+1\right)\le0\\2x-1\le0\end{matrix}\right.\end{matrix}\right.\)\(\)\(\)\(=>\left\{{}\begin{matrix}\left[{}\begin{matrix}x\le-1\\x\ge\dfrac{1}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x\ge-1\\x\le\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\)\(=>-1\le x\le\dfrac{1}{2}\)
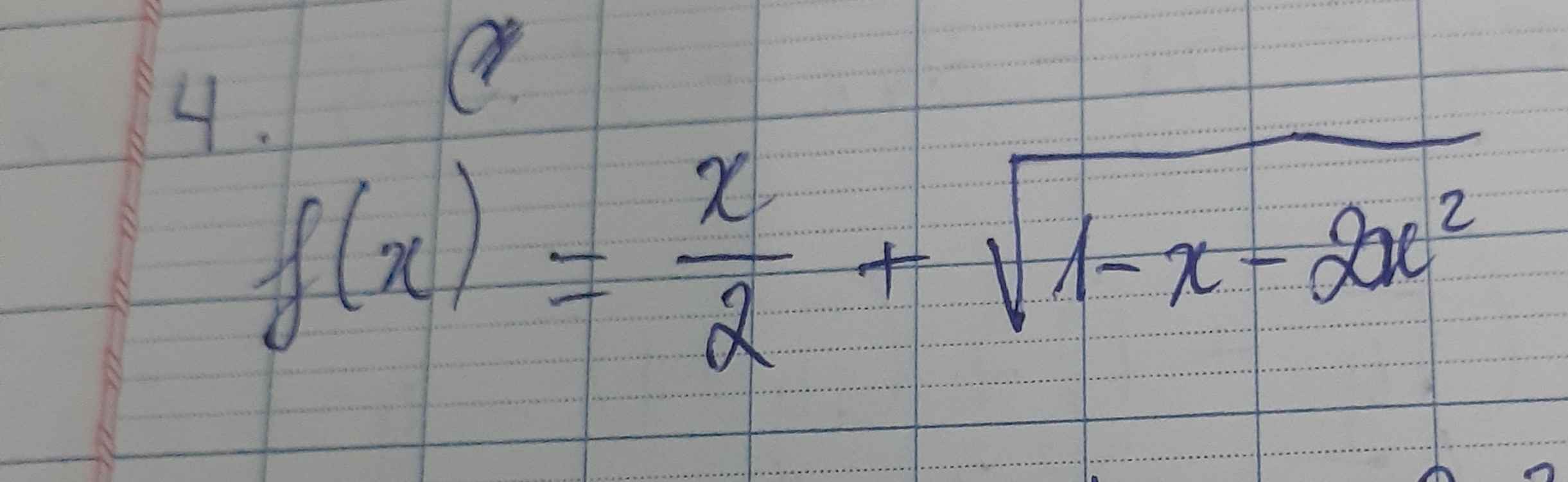
Tìm điều kiện xác định
