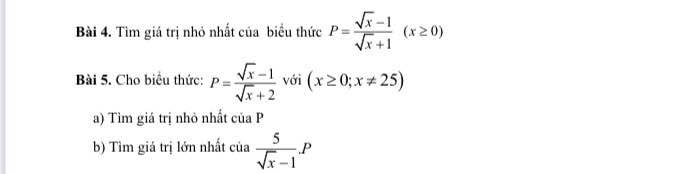4.
\(P=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1-2}{\sqrt{x}+1}=1-\dfrac{2}{\sqrt{x}+1}\ge1-\dfrac{2}{0+1}=-1\)
\(\Rightarrow minP=-1\Leftrightarrow x=0\)
5.
a, \(P=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}=\dfrac{\sqrt{x}+2-3}{\sqrt{x}+2}=1-\dfrac{3}{\sqrt{x}+2}\ge1-\dfrac{3}{0+2}=-\dfrac{1}{2}\)
\(\Rightarrow minP=-\dfrac{1}{2}\Leftrightarrow x=0\)
b, ĐK: \(x\ne1\)
\(\dfrac{5}{\sqrt{x}-1}.P=\dfrac{5}{\sqrt{x}-1}.\dfrac{\sqrt{x}-1}{\sqrt{x}+2}=\dfrac{5}{\sqrt{x}+2}\le\dfrac{5}{0+2}=\dfrac{5}{2}\)
\(\Rightarrow max=\dfrac{5}{2}\Leftrightarrow x=0\)