a: \(\lim_{}\left(\sqrt{5n^2+2n}+\sqrt{n^2+3}\right)\)
\(=\lim_{}\left(n\cdot\sqrt{5+\frac{2}{n}}+n\cdot\sqrt{1+\frac{3}{n^2}}\right)\)
\(=\lim_{}\left\lbrack n\left(\sqrt{5+\frac{2}{n}}\right)+\sqrt{1+\frac{3}{n^2}}\right\rbrack=\lim_{}n\cdot\lim_{}\left(\sqrt{5+\frac{2}{n}}+\sqrt{1+\frac{3}{n^2}}\right)\)
=+∞ vì \(\lim_{}n=+\infty;\lim_{}\left(\sqrt{5+\frac{2}{n}}+\sqrt{1+\frac{3}{n^2}}\right)=\left(\sqrt{5+0}+\sqrt{1+0}\right)=\sqrt5+1>0\)
b: \(\lim_{}\left(\sqrt{16n^4+3n}-4n^2\right)\)
\(=\lim_{}\frac{16n^4+3n-16n^4}{\sqrt{16n^4+3n}+4n^2}=\lim_{}\frac{3n}{n^2\cdot\sqrt{16+\frac{3}{n^3}}+4n^2}\)
\(=\lim_{}\left(\frac{3}{n\cdot\left(\sqrt{16+\frac{3}{n^3}}+4\right)}\right)=+\infty\)
c: \(\lim_{}\frac{n^3+2n+1}{n^2+2n+1}=\lim_{}\frac{n^3\left(1+\frac{2}{n^2}+\frac{1}{n^3}\right)}{n^2\left(1+\frac{2}{n}+\frac{1}{n^2}\right)}\)
\(=\lim_{}\frac{n\cdot\left(1+\frac{2}{n^2}+\frac{1}{n^3}\right)}{1+\frac{2}{n}+\frac{1}{n^2}}=+\infty\)
vì \(\lim_{}n=+\infty;\lim_{}\frac{1+\frac{2}{n^2}+\frac{1}{n^3}}{1+\frac{2}{n}+\frac{1}{n^2}}=\frac11=1\) >0
d: \(\lim_{}\frac{n^2+6}{1-n}=\lim_{}\frac{n^2\left(1+\frac{6}{n}\right)}{n\left(-1+\frac{1}{n}\right)}=\lim_{}\left\lbrack n\cdot\frac{1+\frac{6}{n}}{-1+\frac{1}{n}}\right\rbrack\)
=-∞ vì \(\lim_{}n=+\infty;\lim_{}\frac{1+\frac{6}{n}}{-1+\frac{1}{n}}=\frac{1+0}{-1+0}=-1<0\)
e: \(\lim_{}\left(n^4+6n+3\right)=\lim_{}\left\lbrack n^4\cdot\left(1+\frac{6}{n^3}+\frac{3}{n^4}\right)\right\rbrack\)
\(=+\infty\) vì \(\lim_{}n^4=+\infty;\lim_{}1+\frac{6}{n^3}+\frac{3}{n^4}=1+0+0=1>0\)
g: \(\lim_{}\frac{\sqrt{n^2+3n}-2}{n+1}=\lim_{}\frac{n\left(\sqrt{1+\frac{3}{n}}-\frac{2}{n}\right)}{n\left(1+\frac{1}{n}\right)}=\lim_{}\left(\frac{\sqrt{1+\frac{3}{n}}-\frac{2}{n}}{1+\frac{1}{n}}\right)\)
\(=\frac11=1\)

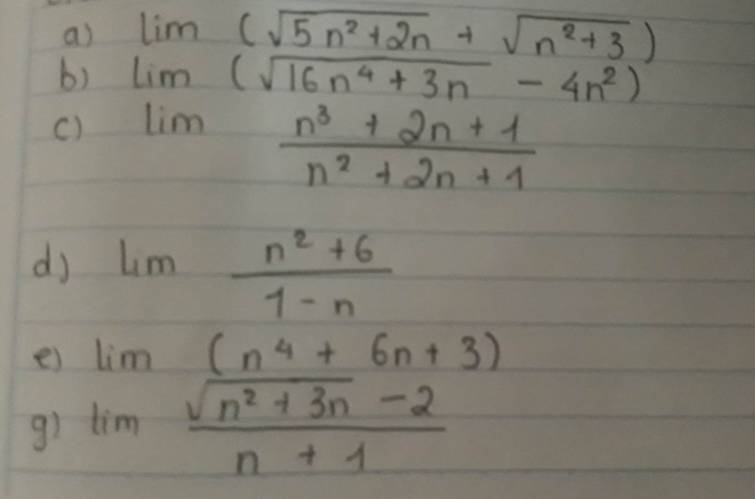 Giúp emm!
Giúp emm!



















 giúp vs
giúp vs giúp vs
giúp vs