ĐK: \(x\ge0\)
TH1: \(m\le0\Rightarrow\) phương trình vô nghiệm.
TH2: \(m>0\)
\(pt\Leftrightarrow\sqrt{x}+2=\dfrac{6}{m}\)
\(\Leftrightarrow\sqrt{x}=\dfrac{6-2m}{m}\)
Phương trình có nghiệm khi: \(\dfrac{6-2m}{m}\ge0\Leftrightarrow6-2m\ge0\Leftrightarrow m\le3\).
\(\Rightarrow0< m\le3\)
Mà \(m\in Z\Rightarrow m\in\left\{1;2;3\right\}\).
\(P=\dfrac{6}{\sqrt{x}+2}\left(đk:x\ge0\right)=m\in Z\)
\(\Rightarrow\sqrt{x}+2\inƯ\left(6\right)=\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
\(\Rightarrow x\in\left\{0;1;16\right\}\)
\(\Rightarrow m\in\left\{1;2;3\right\}\)
Để P nguyên thì \(6⋮\sqrt{x}+2\)
\(\Leftrightarrow\sqrt{x}+2\in\left\{2;3;6\right\}\)
hay \(x\in\left\{0;1;16\right\}\)
\(\Leftrightarrow m\in\left\{3;2;1\right\}\)

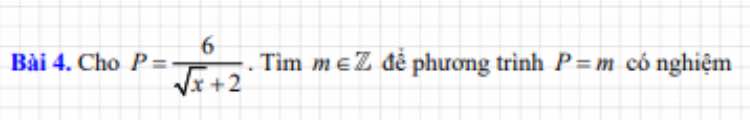











![[IMG]](https://cdn.lazi.vn/storage/uploads/edu/exercise/1636124630_lazi_229734.jpeg)









