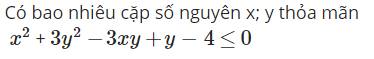`***1)`
`a)3/(1-4x)=2/(4x+1)-(8+6x)/(16x^2-1)(x\ne+-1/4)`
`3/(4x-1)+2/(4x+1)-(8+6x)/((4x+1)(4x-1))=0`
`(3(4x+1))/((4x+1)(4x-1))+(2(4x-1))/((4x+1)(4x-1))-(8+6x)/((4x+1)(4x-1))=0`
`3(4x+1)+2(4x-1)-(8+6x)=0`
`12x+3+8x-2-8-6x=0`
`14x-7=0`
`14x=7`
`x=7/14`
`x=1/2(N)`
Vậy: `x=1/2`
`b)3/(5x-1)+2/(3-5x)=4/((1-5x)(5x-3)(x\ne1/5;x\ne3/5)`
`3/(5x-1)+2/(3-5x)=4/((5x-1)(3-5x))`
`(3(3-5x))/((5x-1)(3-5x))+(2(5x-1))/((5x-1)(3-5x))=4/((5x-1)(3-5x))`
`3(3-5x)+2(5x-1)=4`
`9-15x+10x-2=4`
`-5x+7=4`
`5x=7-4`
`5x=3`
`x=3/5(L)`
Vậy phương trình vô nghiệm
Câu `1`
$ a, \frac{3}{1-4x} = \frac{2}{4x+1} - \frac{8+6x}{16x^2-1}$ (Điều kiện xác định: `x \ne +- 1/4\)` $ \frac{-3(4x + 1)}{(4x - 1)(4x + 1)} = \frac{2(4x - 1)}{(4x - 1)(4x + 1)} - \frac{8 + 6x}{(4x - 1)(4x + 1)} $ ` -3(4x + 1) = 2(4x - 1) - (8 + 6x) ` ` -12x - 3 = 8x - 2 - 8 - 6x` ` -12x - 3 = 2x - 10 ` $ -14x = -7 \Rightarrow x = \frac{1}{2}$ (Thỏa mãn điều kiện)
Câu 3a)
\(\dfrac{x+6}{x-5}+\dfrac{x-5}{x+6}=\dfrac{2x^2-23x+61}{x^2+x-30}\)
\(\rArr\dfrac{\left(x+6\right)^2+\left(x-5\right)^2}{\left(x+6\right)\left(x-5\right)}=\dfrac{2x^2+23x+61}{\left(x+6\right)\left(x-5\right)}\)
\(\rArr\dfrac{2x^2+2x+61}{\left(x+6\right)\left(x-5\right)}=\dfrac{2x^2+23x+61}{\left(x+6\right)\left(x-5\right)}\)
\(\rArr2x^2+2x+61=2x^2+23+61\)
\(\rArr-21x=0\)
\(\rArr x=0\) \((\) Điều kiện xác định: \(x\ne5,x\ne-6\) \()\)
Vậy \(x=0\)
Bài 5:
a: ĐKXĐ: x≠-2
Ta có: \(1+\frac{1}{x+2}=\frac{12}{x^3+8}\)
=>\(1+\frac{1}{x+2}=\frac{12}{\left(x+2\right)\left(x^2-2x+4\right)}\)
=>\(\frac{x^3+8}{\left(x+2\right)\left(x^2-2x+4\right)}+\frac{x^2-2x+4}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{12}{\left(x+2\right)\left(x^2-2x+4\right)}\)
=>\(x^3+8+x^2-2x+4=12\)
=>\(x^3+x^2-2x=0\)
=>\(x\left(x^2+x-2\right)=0\)
=>x(x+2)(x-1)=0
=>\(\left[\begin{array}{l}x=0\\ x+2=0\\ x-1=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=0\left(nhận\right)\\ x=-2\left(loại\right)\\ x=1\left(nhận\right)\end{array}\right.\)
b: ĐKXĐ: x<>2/7
Ta có: \(\left(2x+3\right)\left(\frac{3x+8}{2-7x}+1\right)=\left(x-5\right)\left(\frac{3x+8}{2-7x}+1\right)\)
=>\(\left(2x+3\right)\cdot\frac{3x+8+2-7x}{2-7x}=\left(x-5\right)\cdot\frac{3x+8+2-7x}{2-7x}\)
=>\(\left(2x+3\right)\cdot\frac{-4x+10}{2-7x}=\left(x-5\right)\cdot\frac{-4x+10}{2-7x}\)
=>\(\left(2x+3\right)\left(-4x+10\right)-\left(x-5\right)\left(-4x+10\right)=0\)
=>(-4x+10)(2x+3-x+5)=0
=>-2(2x-5)(x+8)=0
=>(2x-5)(x+8)=0
=>\(\left[\begin{array}{l}2x-5=0\\ x+8=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac52\left(nhận\right)\\ x=-8\left(nhận\right)\end{array}\right.\)
Bài 4:
a: ĐKXĐ: x∉{2;-1}
Ta có: \(\frac{x+2}{x+1}+\frac{3}{x-2}=\frac{3}{x^2-x-2}+1\)
=>\(\frac{x+2}{x+1}+\frac{3}{x-2}=\frac{3}{\left(x-2\right)\left(x+1\right)}+1\)
=>\(\frac{\left(x+2\right)\left(x-2\right)+3\left(x+1\right)}{\left(x-2\right)\left(x+1\right)}=\frac{3}{\left(x-2\right)\left(x+1\right)}+\frac{\left(x-2\right)\left(x+1\right)}{\left(x-2\right)\left(x+1\right)}\)
=>(x-2)(x+2)+3(x+1)=3+(x-2)(x+1)
=>\(x^2-4+3x+3=3+x^2-x-2\)
=>3x-1=-x+1
=>4x=2
=>\(x=\frac12\) (nhận)
b: ĐKXĐ: x∉{5;-6}
Ta có: \(\frac{x+6}{x-5}+\frac{x-5}{x+6}=\frac{2x^2+23x+61}{x^2+x-30}\)
=>\(\frac{x+6}{x-5}+\frac{x-5}{x+6}=\frac{2x^2+23x+61}{\left(x+6\right)\left(x-5\right)}\)
=>\(\frac{\left(x+6\right)^2+\left(x-5\right)^2}{\left(x+6\right)\left(x-5\right)}=\frac{2x^2+23x+61}{\left(x+6\right)\left(x-5\right)}\)
=>\(\left(x+6\right)^2+\left(x-5\right)^2=2x^2+23x+61\)
=>\(x^2+12x+36+x^2-10x+25=2x^2+23x+61\)
=>2x+61=23x+61
=>-21x=0
=>x=0(nhận)
Bài 3:
a: ĐKXĐ: x∉{5;-6}
Ta có: \(\frac{x+6}{x-5}+\frac{x-5}{x+6}=\frac{2x^2+23x+61}{x^2+x-30}\)
=>\(\frac{x+6}{x-5}+\frac{x-5}{x+6}=\frac{2x^2+23x+61}{\left(x+6\right)\left(x-5\right)}\)
=>\(\frac{\left(x+6\right)^2+\left(x-5\right)^2}{\left(x+6\right)\left(x-5\right)}=\frac{2x^2+23x+61}{\left(x+6\right)\left(x-5\right)}\)
=>\(\left(x+6\right)^2+\left(x-5\right)^2=2x^2+23x+61\)
=>\(x^2+12x+36+x^2-10x+25=2x^2+23x+61\)
=>2x+61=23x+61
=>-21x=0
=>x=0(nhận)
b: ĐKXĐ: x∉{3;-3}
Ta có: \(\frac{x^2-x}{x+3}-\frac{x_{}^2}{x-3}=\frac{7x^2-3x}{9-x^2}\)
=>\(\frac{\left(x^2-x\right)\left(x-3\right)-x^2\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}=\frac{-7x^2+3x}{\left(x-3\right)\left(x+3\right)}\)
=>\(\left(x^2-x\right)\left(x-3\right)-x^2\left(x+3\right)=-7x^2+3x\)
=>\(x^3-3x^2-x^2+3x-x^3-3x^2+7x^2-3x=0\)
=>0x=0(luôn đúng)
Vậy: x∉{3;-3}
Bài 2:
a: ĐKXĐ: x∉{-1;2}
ta có: \(\frac{x+2}{x+1}+\frac{3}{x-2}=\frac{3}{x^2-x-2}+1\)
=>\(\frac{\left(x+2\right)\left(x-2\right)+3\left(x+1\right)}{\left(x-2\right)\left(x+1\right)}=\frac{3+x^2-x-2}{\left(x-2\right)\left(x+1\right)}\)
=>\(\left(x+2\right)\left(x-2\right)+3\left(x+1\right)=x^2-x+1\)
=>\(x^2-4+3x+3=x^2-x+1\)
=>3x-1=-x+1
=>4x=2
=>\(x=\frac12\) (nhận)
b: ĐKXĐ: x∉{0;2}
ta có: \(\frac{5-x}{4x^2-8x}+\frac78=\frac{x-1}{2x\left(x-2\right)}+\frac{1}{8x-16}\)
=>\(\frac{5-x}{4x\left(x-2\right)}+\frac78=\frac{x-1}{2x\left(x-2\right)}+\frac{1}{8\left(x-2\right)}\)
=>\(\frac{4\left(5-x\right)}{16x\left(x-2\right)}+\frac{7\cdot2x\cdot\left(x-2\right)}{8\cdot2x\cdot\left(x-2\right)}=\frac{8\left(x-1\right)}{8\cdot2x\cdot\left(x-2\right)}+\frac{2x}{8\cdot2x\cdot\left(x-2\right)}\)
=>4(5-x)+14x(x-2)=8(x-1)+2x
=>\(20-4x+14x^2-28x=8x-8+2x\)
=>\(14x^2-32x+20-10x+8=0\)
=>\(14x^2-42x+28=0\)
=>\(x^2-3x+2=0\)
=>(x-2)(x-1)=0
=>x=2(loại) hoặc x=1(nhận)
Bài 1:
a: ĐKXĐ: x∉{1/4;-1/4}
ta có: \(\frac{3}{1-4x}=\frac{2}{4x+1}-\frac{6x+8}{16x^2-1}\)
=>\(\frac{-3}{4x-1}-\frac{2}{4x+1}=\frac{-6x-8}{\left(4x-1\right)\left(4x+1\right)}\)
=>\(\frac{-3\left(4x+1\right)}{\left(4x-1\right)\left(4x+1\right)}-\frac{2\left(4x-1\right)}{\left(4x+1\right)\left(4x-1\right)}=\frac{-6x-8}{\left(4x-1\right)\left(4x+1\right)}\)
=>-3(4x+1)-2(4x-1)=-6x-8
=>-12x-3-8x+2=-6x-8
=>-20x-1=-6x-8
=>-14x=-7
=>x=1/2(nhận)
b: ĐKXĐ: x∉{1/5;3/5}
Ta có: \(\frac{3}{5x-1}+\frac{2}{3-5x}=\frac{4}{\left(1-5x\right)\left(5x-3\right)}\)
=>\(\frac{3}{5x-1}-\frac{2}{5x-3}=\frac{-4}{\left(5x-1\right)\left(5x-3\right)}\)
=>\(\frac{3\left(5x-3\right)}{\left(5x-1\right)\left(5x-3\right)}-\frac{2\left(5x-1\right)}{\left(5x-1\right)\left(5x-3\right)}=\frac{-4}{\left(5x-1\right)\left(5x-3\right)}\)
=>3(5x-3)-2(5x-1)=-4
=>15x-9-10x+2=-4
=>5x-7=-4
=>5x=3
=>x=3/5(loại)
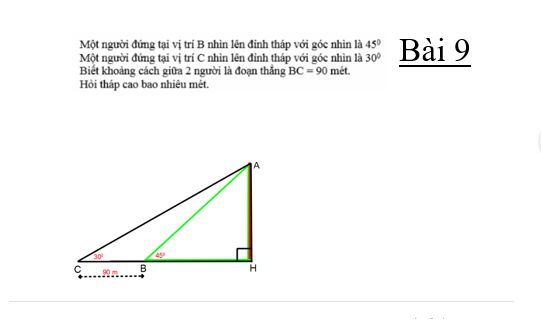giúp em với ạ. Em cảm ơn ạ
