52.
\(AC=ABlog_23\Leftrightarrow log_b6=log_a6.log_23=\dfrac{log_b6}{log_ba}.log_23\)
\(\Rightarrow log_ba=log_23\)\(\Rightarrow a=b^{log_23}=3^{log_2b}\)
\(\Rightarrow log_3a=log_2b\)
D
54.
Do \(y=a^x\) nghịch biến nên \(0< a< 1\)
\(y=4^x\Rightarrow x=log_4y\)
\(y=a^x\Rightarrow x=log_ay\)
\(AN=2AM\Rightarrow\left|log_ax\right|=2\left|log_4x\right|\)
\(\Leftrightarrow-log_ax=log_2x\)
\(\Rightarrow log_{a^{-1}}=log_2x\)
\(\Rightarrow a^{-1}=2\)
\(\Rightarrow a=\dfrac{1}{2}\)















 Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ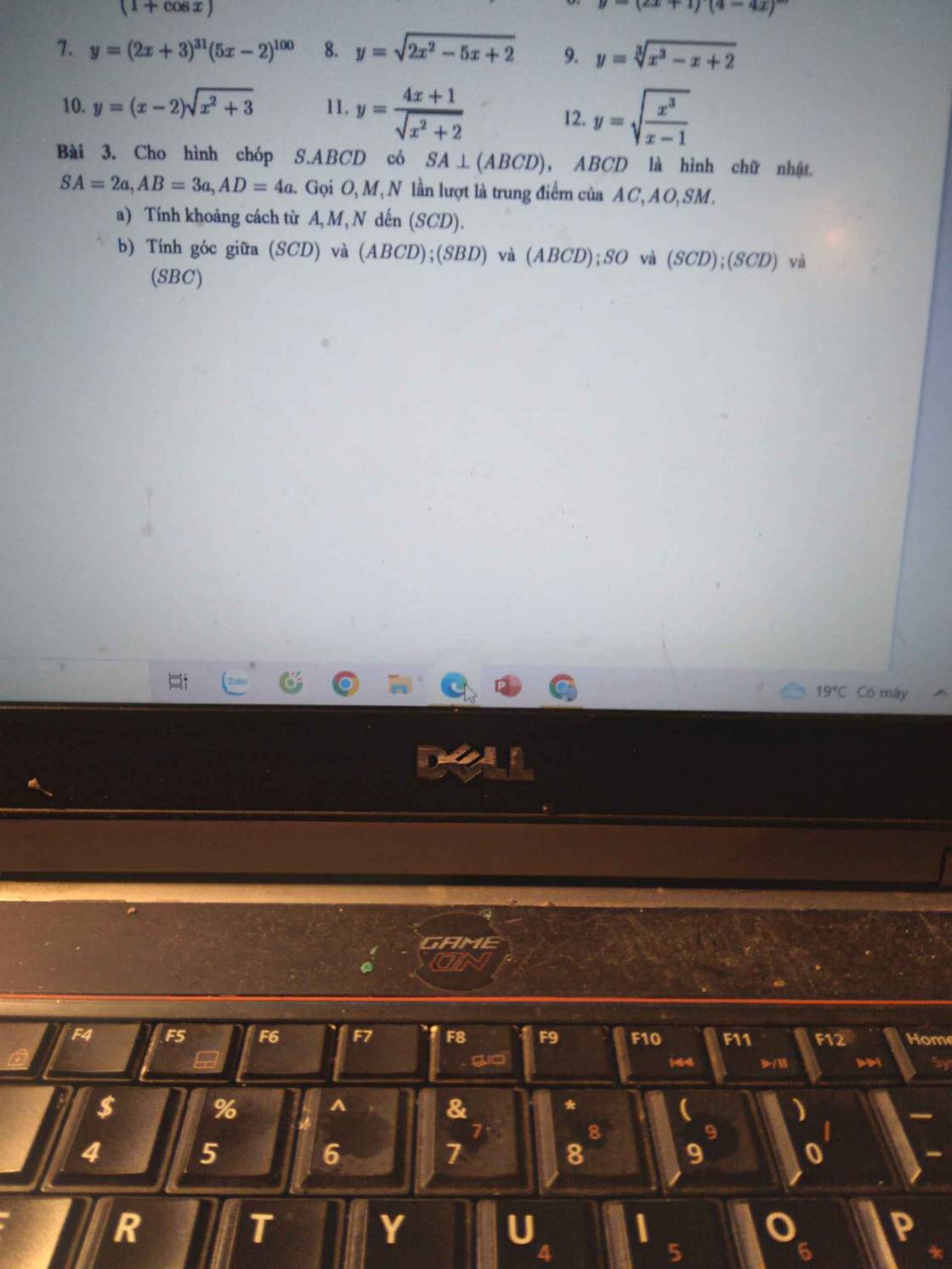 Giúp em bài 3 với ạ. Em cảm ơn ạ
Giúp em bài 3 với ạ. Em cảm ơn ạ









