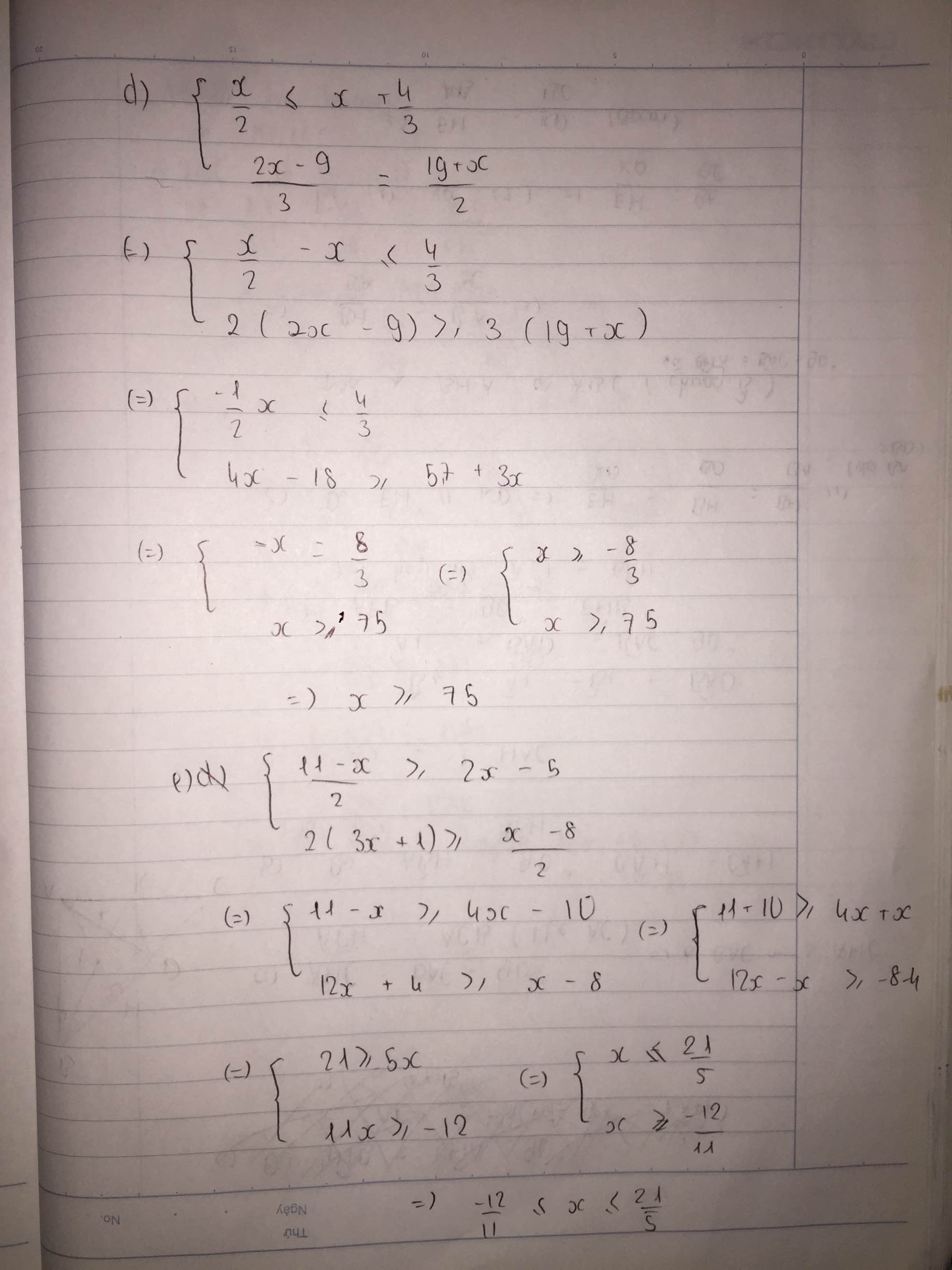d. \(\left\{{}\begin{matrix}\dfrac{x}{2}\le x+\dfrac{4}{3}\\\dfrac{2x-9}{3}< \dfrac{19+x}{2}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}3x\le6x+8\\4x-18< 57+3x\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}-8\le3x\\x< 75\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{8}{3}\le x\\x< 75\end{matrix}\right.\)
\(\Rightarrow\dfrac{-8}{3}\le x< 75\)
e. \(\left\{{}\begin{matrix}\dfrac{11-x}{2}\ge2x-5\\2\left(3x+1\right)\ge\dfrac{x-8}{2}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}11-x\ge4x-10\\4\left(3x+1\right)\ge x-8\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}21\ge5x\\12x+4\ge x-8\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}21\ge5x\\11x\ge-12\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{21}{5}\ge x\\x\ge-\dfrac{12}{11}\end{matrix}\right.\)\(\Rightarrow\dfrac{-12}{11}\le x< \dfrac{21}{5}\)