10.
\(\dfrac{sin3x-cos3x}{sinx+cosx}=\dfrac{3sinx-4sin^3x-\left(4cos^3x-3cosx\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sin^3x+cos^3x\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)}{sinx+cosx}\)
\(=\dfrac{3\left(sinx+cosx\right)-4\left(sinx+cosx\right)\left(1-sinx.cosx\right)}{sinx+cosx}\)
\(=\dfrac{\left(sinx+cosx\right)\left(3-4+4sinx.cosx\right)}{sinx+cosx}\)
\(=-1+4sinx.cosx\)
\(=2sin2x-1\)
11.
\(tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\dfrac{1+cos\left(\dfrac{\pi}{2}+x\right)}{sin\left(\dfrac{\pi}{2}+x\right)}=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{1+sin\left(-x\right)}{cos\left(-x\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{1-sinx}{cosx}=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\dfrac{sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}-2sin\dfrac{x}{2}cos\dfrac{x}{2}}{cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{\left(cos\dfrac{x}{2}-sin\dfrac{x}{2}\right)^2}{\left(cos\dfrac{x}{2}-sin\dfrac{x}{2}\right)\left(cos\dfrac{x}{2}+sin\dfrac{x}{2}\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{cos\dfrac{x}{2}-sin\dfrac{x}{2}}{cos\dfrac{x}{2}+sin\dfrac{x}{2}}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).\dfrac{cos\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)}{sin\left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)}\)
\(=tan\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right).cot\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right)\)
\(=1\)
12.
\(cot2x+\dfrac{1}{sin2x}+tanx=\dfrac{cos2x}{sin2x}+\dfrac{1}{sin2x}+tanx\)
\(=\dfrac{cos2x+1}{sin2x}+\dfrac{sinx}{cosx}=\dfrac{2cos^2x-1+1}{2sinx.cosx}+\dfrac{sinx}{cosx}\)
\(=\dfrac{2cos^2x}{2sinx.cosx}+\dfrac{sinx}{cosx}=\dfrac{cosx}{sinx}+\dfrac{sinx}{cosx}\)
\(=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}\)
\(=\dfrac{2}{2sinx.cosx}=\dfrac{2}{sin2x}\)
13.
\(\dfrac{1-cos2x+sin2x}{1+cos2x+sin2x}.cotx=\dfrac{1-\left(1-2sin^2x\right)+2sinx.cosx}{1+2cos^2x-1+2sinx.cosx}.cotx\)
\(=\dfrac{2sin^2x+2sinx.cosx}{2cos^2x+2sinx.cosx}.cotx\)
\(=\dfrac{2sinx\left(sinx+cosx\right)}{2cosx\left(sinx+cosx\right)}.cotx\)
\(=\dfrac{sinx}{cosx}.cotx=tanx.cotx\)
\(=1\)
14.
\(\dfrac{2\left(sin2x+2cos^2x-1\right)}{cosx-sinx-cos3x+sin3x}=\dfrac{2\left(sin2x+cos2x\right)}{\left(cosx-cos3x\right)+\left(sin3x-sinx\right)}\)
\(=\dfrac{2\left(sin2x+cos2x\right)}{2sin2x.sinx+2cos2x.sinx}\)
\(=\dfrac{2\left(sin2x+cos2x\right)}{2sinx\left(sin2x+cos2x\right)}\)
\(=\dfrac{1}{sinx}\)
15.
\(\dfrac{1}{sin2x}+\dfrac{1}{sin4x}+\dfrac{1}{sin8x}+cot8x=\dfrac{1}{sin2x}+\dfrac{1}{sin4x}+\dfrac{1}{sin8x}+\dfrac{cos8x}{sin8x}\)
\(=\dfrac{1}{sin2x}+\dfrac{1}{sin4x}+\dfrac{1+2cos^24x-1}{2sin4x.cos4x}\)
\(=\dfrac{1}{sin2x}+\dfrac{1}{sin4x}+\dfrac{2cos^24x}{2sin4x.cos4x}\)
\(=\dfrac{1}{sin2x}+\dfrac{1}{sin4x}+\dfrac{cos4x}{sin4x}\)
\(=\dfrac{1}{sin2x}+\dfrac{1+cos4x}{sin4x}=\dfrac{1}{sin2x}+\dfrac{1+2cos^22x-1}{2sin2x.cos2x}\)
\(=\dfrac{1}{sin2x}+\dfrac{cos2x}{sin2x}\)
\(=\dfrac{1+cos2x}{sin2x}=\dfrac{1+2cos^2x-1}{2sinx.cosx}\)
\(=\dfrac{cosx}{sinx}=cotx\)
16.
\(-\dfrac{\pi}{4}< x< \dfrac{\pi}{4}\Rightarrow\left\{{}\begin{matrix}sinx+cosx>0\\sinx-cosx< 0\end{matrix}\right.\)
\(\sqrt{1-sin2x}+\sqrt{1+sin2x}\)
\(=\sqrt{sin^2x+cos^2x-2sinx.cosx}+\sqrt{sin^2x+cos^2x-2sinx.cosx}\)
\(=\sqrt{\left(sinx-cosx\right)^2}+\sqrt{\left(sinx+cosx\right)^2}\)
\(=\left|sinx-cosx\right|+\left|sinx+cosx\right|\)
\(=cosx-sinx+sinx+cosx\)
\(=2cosx\)
17.
\(0< x< \dfrac{\pi}{4}\Rightarrow\left\{{}\begin{matrix}sin\dfrac{x}{2}+cos\dfrac{x}{2}>0\\sin\dfrac{x}{2}-cos\dfrac{x}{2}< 0\end{matrix}\right.\)
\(\sqrt{1+sinx}+\sqrt{1-sinx}\)
\(=\sqrt{sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}+2sin\dfrac{x}{2}cos\dfrac{x}{2}}+\sqrt{sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}-2sin\dfrac{x}{2}cos\dfrac{x}{2}}\)
\(=\sqrt{\left(sin\dfrac{x}{2}+cos\dfrac{x}{2}\right)^2}+\sqrt{\left(sin\dfrac{x}{2}-cos\dfrac{x}{2}\right)^2}\)
\(=\left|sin\dfrac{x}{2}+cos\dfrac{x}{2}\right|+\left|sin\dfrac{x}{2}-cos\dfrac{x}{2}\right|\)
\(=sin\dfrac{x}{2}+cos\dfrac{x}{2}+cos\dfrac{x}{2}-sin\dfrac{x}{2}\)
\(=2cos\dfrac{x}{2}\)
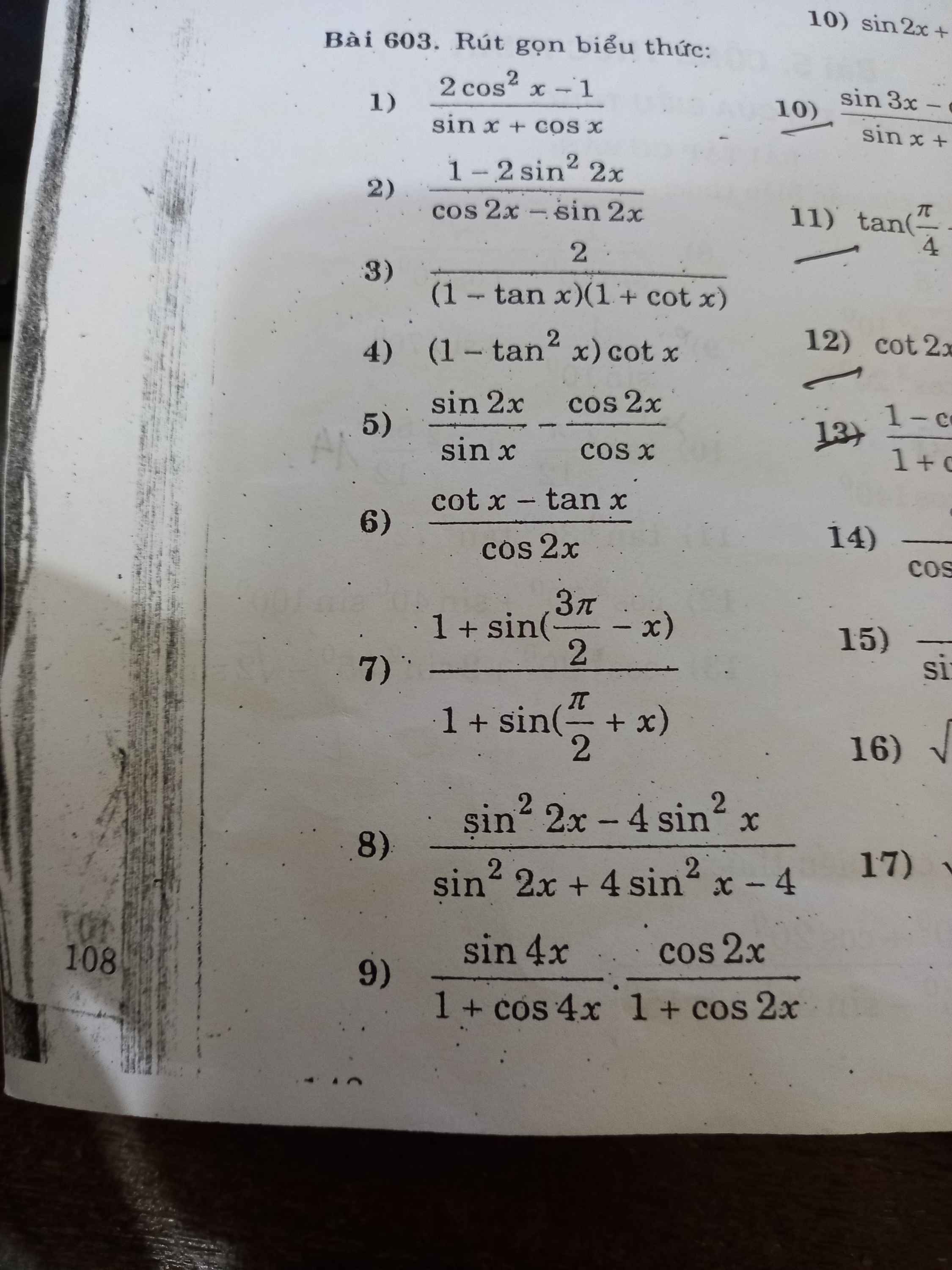
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn