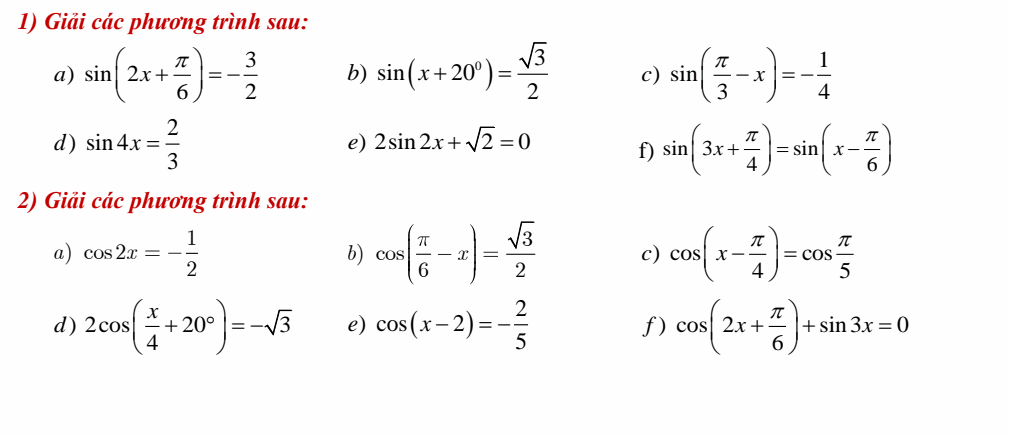Không gian mẫu: \(\left(\Omega\right)=8^5\)
Gọi A là biến cố: "chọn ra 5 số có tích bằng 2520"
Ta chọn ra \(5\) số có tích bằng \(2520\):
- chọn ra \(2\) số \(5\) và \(7\) có \(1\) cách
-chọn ra \(3\) số còn lại để tích của chúng là \(72\)
gọi 3 số cần tìm là \(a,b,c\)
vì vai trò 3 số như nhau nên ta xét các trường hợp của \(a\):
TH1: \(a=1\)
\(b,c\) không có cách chọn
TH2: \(a=2\)
\(\Rightarrow\left(b;c\right)=\left(6;6\right)\) và các hoán vị của \(\left(9;4\right)\)
TH3: \(a=3\)
\(\Rightarrow\left(b;c\right)=\) các hoán vị của \(\left(3;8\right)\) và các hoán vị của \(\left(4;6\right)\)
TH4: \(a=6\)
\(\Rightarrow\left(b;c\right)=\left(2;6\right)\) và các hoán vị; \(\left(3;4\right)\) và các hoán vị
TH5: \(a=8\)
\(\Rightarrow\left(b;c\right)=\left(3;3\right)\)
Vậy số cách chọn \(3\) cặp số \(a,b,c\) là: \(3+4+4+1=12\)
-Hoán vị \(5,7,a,b,c\) có \(5!\) cách
=> có 5!.12=1440 cách lập số có 5 chữ số mà tích của chúng bằng 2520
=> \(P\left(A\right)\) = \(\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{45}{1024}\)
=> a+b = 1069